
Aerei e città: un esercizio di combinatoria
Oggi ci troviamo di fronte a un altro esercizio di combinatoria, speriamo che possa risultare utile e accattivante. Sarai in grado di trovare la risposta prima di leggere la soluzione?
Problema. Supponiamo di considerare un po’ di città, e una rete di traffico aereo tra queste città. Con volo diretto tra due città si intende una tratta aerea, sia in andata che in ritorno, che permette di viaggiare tra i due paesi senza fermate intermedie. Una città è raggiungibile da un’altra città se esiste una successione di scali e di voli diretti che permettono di passare, in modo indiretto, dalla seconda alla prima. Ecco qui il testo:
In una regione sono presenti 17 città; ognuna di queste è collegata con alcune delle altre mediante un volo diretto (andata e ritorno). Supponiamo inoltre che tra due città possa essere presente al massimo una tratta di volo diretto, e non è detto che questa ci sia. Determinare il massimo numero di voli diretti che è possibile programmare affinché esistano due città non raggiungibili l’una dall’altra.
Soluzione. Il problema enunciato è ben immaginabile dal punto di vista geometrico. Possiamo figurarci le città come punti del piano, e i voli diretti come segmenti che congiungono i vari punti. L’ipotesi che suona come “tra due città può essere presente al massimo una tratta di volo diretto, e non è detto che questa ci sia” ci dice semplicemente che al più un segmento congiunge due dei punti considerati. Riletto il problema in questi termini possiamo aspettarci una situazione di questo tipo:
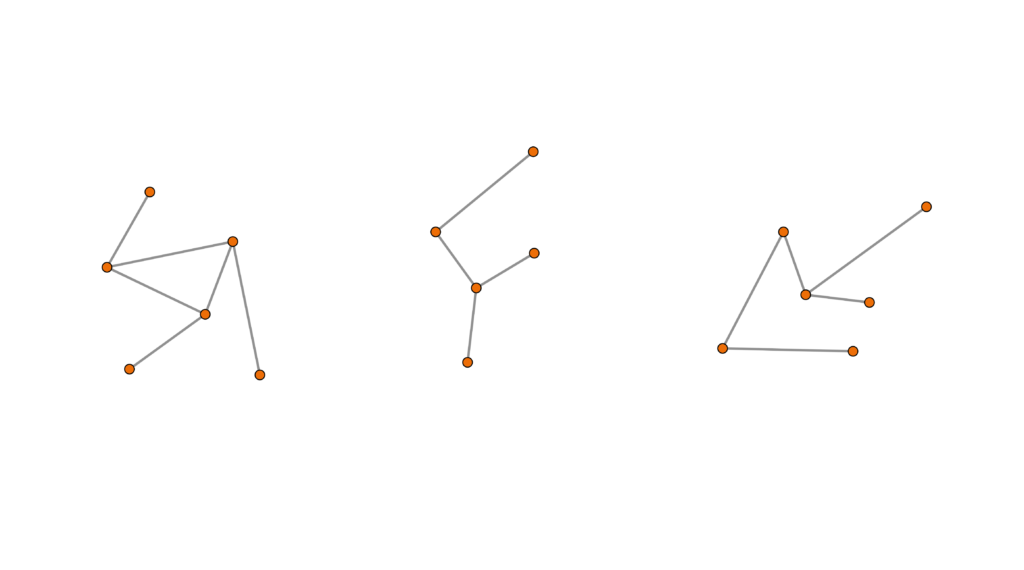
Cosa ci domanda l’esercizio? Ci chiede fondamentalmente di metterci in una situazione in cui esistano almeno due pezzi connessi distinti. Spieghiamoci meglio. Fissato un punto \(P\) del piano, possiamo considerare l’insieme di tutti i punti che sono raggiungibili a partire da \(P\). In questo modo le città vengono ripartite in vari sottoinsiemi, che chiameremo per chiari motivi componenti connesse del disegno. Ad esempio, nella situazione sopra, le componenti connesse sono 3. In conclusione, la richiesta “esistono due città non raggiungibili l’una dall’altra” si traduce nell’esistenza di almeno 2 componenti connesse distinte; infatti, se ne esistesse una soltanto, ogni città sarebbe raggiungibile da qualsiasi altra.
Vogliamo tuttavia massimizzare il numero di voli che è possibile programmare in questa situazione. Quante possono essere le componenti connesse del disegno? L’osservazione chiave è che queste devono essere necessariamente 2. Supponiamo infatti che queste siano almeno 3; consideriamo una città nella seconda componente e una nella terza, e aggiungiamo il volo diretto che congiunge queste due. La situazione che abbiamo ottenuto rispetta ancora le ipotesi (la prima componente del disegno fa ancora pezzo a sé!), tuttavia è presente un volo diretto in più. Dunque la configurazione precedente non poteva realizzare il massimo numero di voli diretti! In conclusione, le componenti connesse devono essere esattamente 2. Qui in figura è schematizzata l’aggiunta dal volo extra, sempre in riferimento all’esempio precedente.
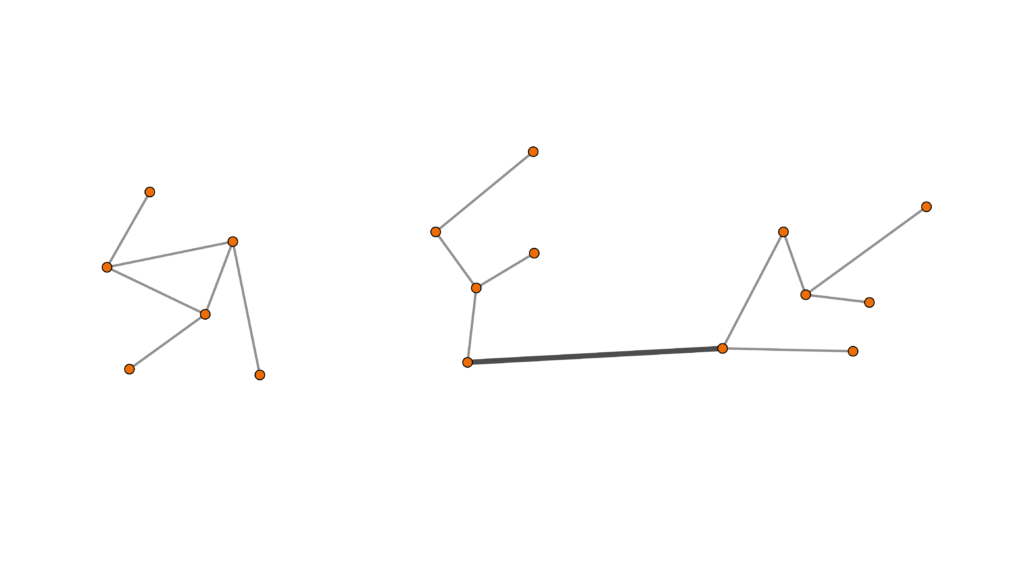
Nella prima componente connessa saranno presenti \(n\) città, e di conseguenza nella seconda ce ne saranno \(17-n\). I vincoli su \(n\) sono dati da \(1 \le n \le 16\), in quanto se \(n=0\) oppure \(n=17\) di pezzi connessi ne avremmo uno soltanto. Vogliamo capire qual è il migliore \(n\) per i nostri propositi. Fissato \(n\), per massimizzare il numero di voli diretti non ci resta che considerare tutti i voli diretti possibili nella prima componente, tutti i voli possibili nella seconda, e sommare questi risultati per ottenere il numero di voli totali. Fissiamo l’attenzione sulla prima; quanti segmenti possiamo costruire tra gli \(n\) punti considerati? Si tratta semplicemente del coefficiente binomiale \(\binom{n}{2}\). Infatti, ricordando l’interpretazione del coefficiente binomiale, sappiamo che \(\binom{n}{2}\) altro non è che il numero di modi di scegliere \(2\) oggetti da \(n\) senza che conti l’ordine; un attimo di riflessione ci convince che si tratti esattamente del numero di modi in cui è possibile costruire un segmento dati \(n\) punti. Lo stesso argomento vale per la seconda componente connessa, che ci regala \(\binom{17-n}{2}\) voli diretti disponibili. La somma di questi vale
\(\binom{n}{2} + \binom{17-n}{2}=\)
\(\frac{n(n-1)}{2} + \frac{(17-n)(17-n-1)}{2}=\)
\(n^2 -17n + 136.\)
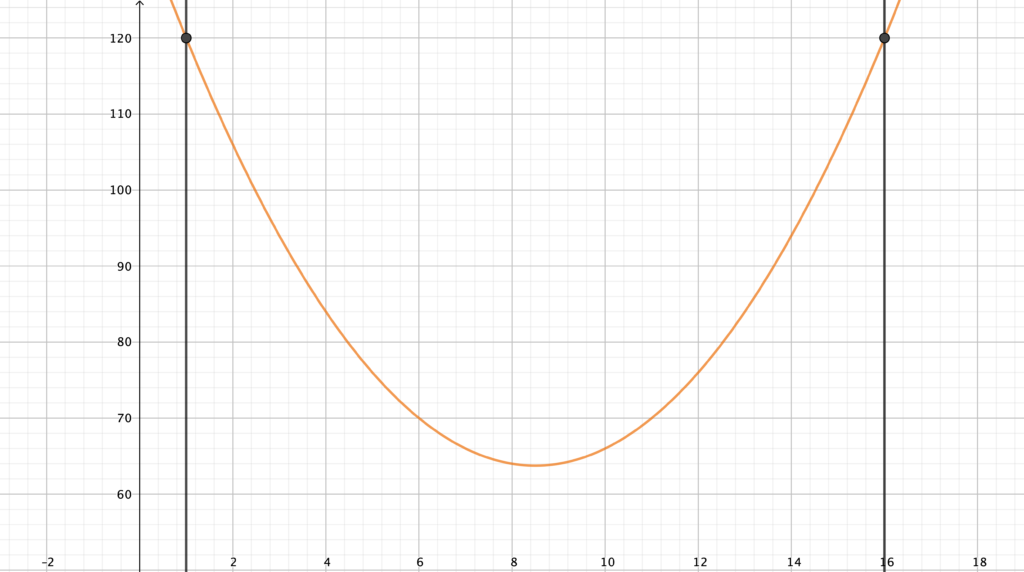
Quello che otteniamo è una parabola con vertice di ascissa (non a caso!) \(17/2=8.5\) e concavità rivolta verso l’alto. Graficamente deduciamo che il massimo sarà ottenuto in uno dei due estremi \(n=1\) oppure \(n=16\). Data la simmetria del problema (o per semplice sostituzione) il valore ottenuto in questi due punti è lo stesso, in particolare si tratta di \(120\). Dunque la situazione ottimale è realizzata quando una sola città sta per i conti suoi, isolata dal resto del mondo, e le altre 16 sono collegate in tutti i modi possibili. Si noti infatti che \(\binom{16}{2}=120\) esplicita chiaramente la situazione in cui sono presenti tutti i voli diretti ammissibili tra 16 delle 17 città. In conclusione, \(120\) è la risposta al problema.
Questo era un esercizio tra aerei e città 😉
Speriamo tu possa aver trovato utile questo nostro articolo.
Se hai domande o commenti non esitare a scrivere qui sotto!
No Comments