DISEQUAZIONI DI SECONDO GRADO

DISEQUAZIONI DI SECONDO GRADO

Risolvere una disequazione di secondo grado $ax^2+bx+c\ge 0$ (al posto di $\ge$ possiamo trovare $\le$, $<$ o $>$) significa trovare quel sottoinsieme $S\subseteq \mathbb{R}$ tale per cui, per ogni numero reale del sottoinsieme $S$, la disuguaglianza è verificata. $S$ prenderà il nome di soluzione della disequazione di secondo grado, e solitamente è un intervallo, un unione di intervalli, tutto $\mathbb{R}$ oppure l’insieme vuoto. In particolare, se $S=\emptyset$ la disequazione si dice impossibile; se invece $S=\mathbb{R}$ la disequazione è sempre verificata. In seguito vedremo esempi di entrambi i casi; prima, però, bisogna imparare come stabilire la soluzione $S$: per farlo, però, ricordiamo la formula risolutiva delle equazioni di secondo grado.

Risolvere un’equazione di secondo grado.

Sia data l’equazione di secondo grado $ax^2+bx+c=0$, dove $a,b,c$ sono numeri reali, con $a\neq 0$. Ricordiamo che si può definire una quantità $\Delta$, chiamata discriminante o delta, che è in grado di stabilire il numero di soluzioni dell’equazione.

$\Delta=b^2-4ac$. Si possono presentare tre casi:

$\Delta >0$ : l’equazione ha due soluzioni reali distinte.
$\Delta =0$: l’equazione ha due soluzioni reali coincidenti.
$\Delta<0$: l’equazione ha zero soluzioni reali.

Nel caso in cui $\Delta\ge 0$, è possibile determinare le soluzioni utilizzando questa formula:

$x_{1,2}=\frac{-b\pm \sqrt{\Delta}}{2a}$.

Nel caso in cui $b$ sia un numero pari è conveniente utilizzare questa formula, chiamata formula ridotta:

$x_{1,2}=\frac{-\frac{b}{2}\pm \sqrt{\frac{\Delta}{4}}}{a}$.

Risolvere una disequazione di secondo grado

Dopo questo ripasso, siamo pronti a risolvere disequazioni di secondo grado.

$ax^2+bx+c\ge0$.

Supponiamo per ora che il coefficiente davanti alla $x^2$ sia positivo, dunque $a>0$.

La cosa importante da ricordare è che fino all’ultimo step dobbiamo disinteressarci del tipo di disuguaglianza che il problema ci propone: i primi tre step sono uguali sia che ci sia un $\ge$, sia che ci sia un $\le$, sia che ci sia un $>$ o $<$.

PRIMO STEP: SOLUZIONE DELL’EQUAZIONE ASSOCIATA.

La prima cosa a cui siamo interessati è capire per quali $x$ il polinomio valga effettivamente $0$, quindi risolviamo l’equazione come visto poco sopra. Dunque si presentano tre casi.

Caso (a)=$\Delta >0$ Troviamo in questo caso le due soluzioni distinte $x_1,x_2$ (supponiamo $x_1$ la più piccola e $x_2$ la più grande).
Caso(b)=$\Delta =0$ In questo caso troviamo le due soluzioni coincidenti $x_1=x_2$. Per non confonderci rinominiamo questa unica soluzione $\bar{x}$.
Caso (c)= $\Delta<0$ In questo caso non c’è nessuna soluzione.

SECONDO STEP: LA RAPPRESENTAZIONE GRAFICA.

I polinomi di secondo grado possono essere rappresentati graficamente come delle parabole, e siccome $a>0$ queste parabole hanno la concavità (in parole povere la “pancia”) verso l’alto. Risolvere la disequazione diventa equivalente a stabilirequando queste parabole “sorpassino” il livello 0. Per fare un disegno utile della parabola è sufficiente sapere quali siano i punti in cui viene toccato il cosiddetto livello zero e quale sia la concavità della parabola (come già detto, verso l’alto). Analizziamo separatamente i tre casi:

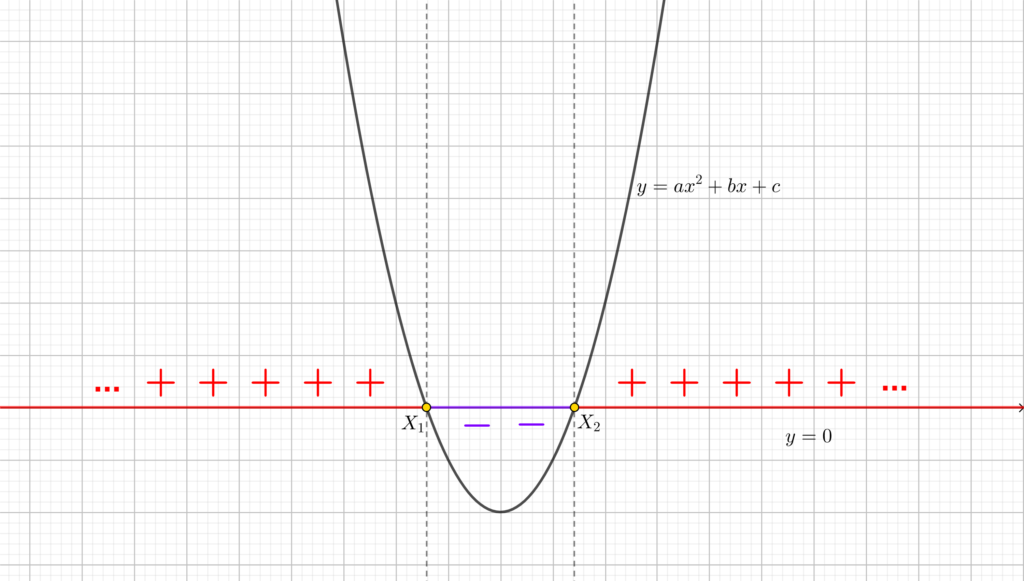
Caso (a) Come già osservato, l’equazione ha due soluzioni distinte $x_1$ e $x_2$, che sono i punti in cui la parabola interseca il livello 0 (nel piano cartesiano la retta $y=0$). Inoltre la concavità è verso l’alto. Possiamo allora fare un disegno di questo tipo, che rappresenta fedelmente il segno della parabola, e dunque del polinomio.

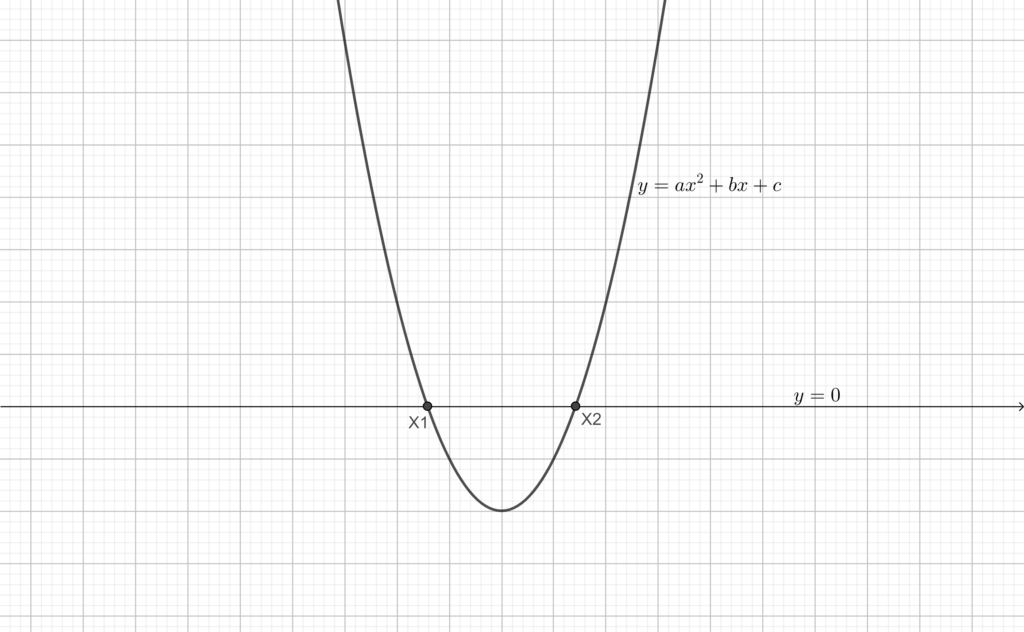
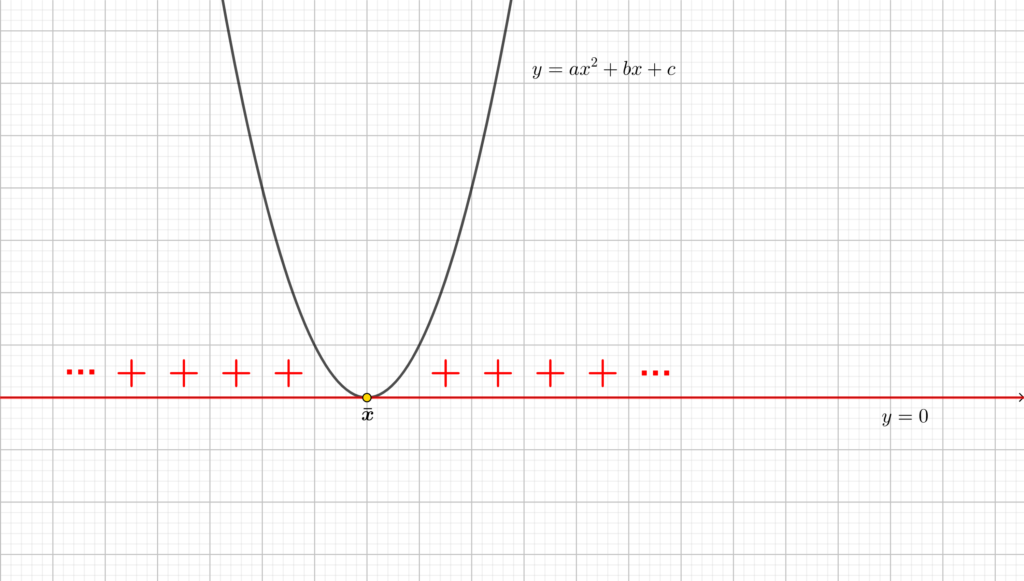
La parabola che rappresenta $ax^2+bx+c$ quando $\Delta$>0 e $a>0$.

Caso (b) In questo caso la parabola interseca l’asse $y=0$ nel solo punto $\bar{x}$, e, come già osservato, la concavità è verso l’alto (perchè $a>0$). La parabola avrà dunque il seguente grafico.

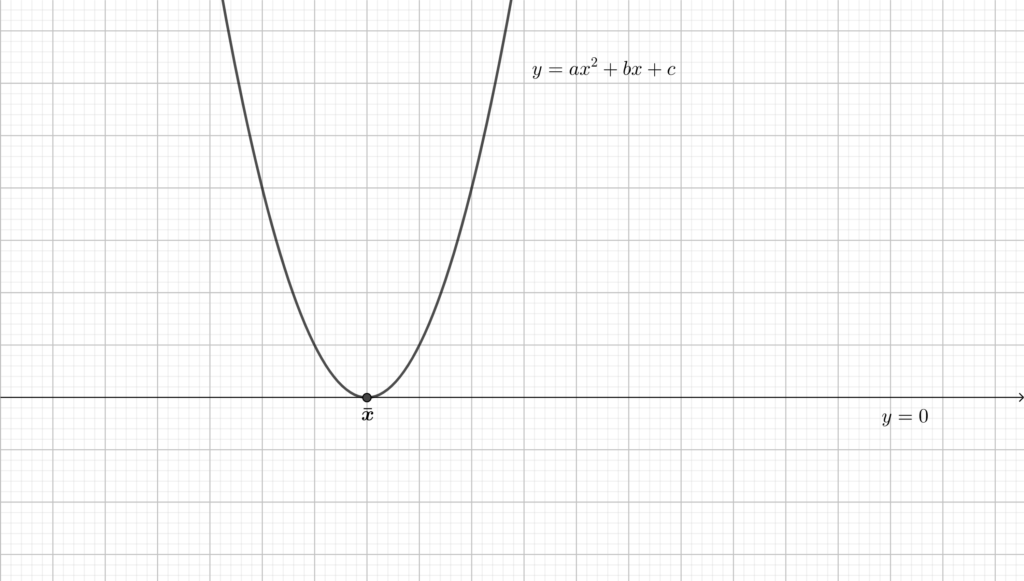
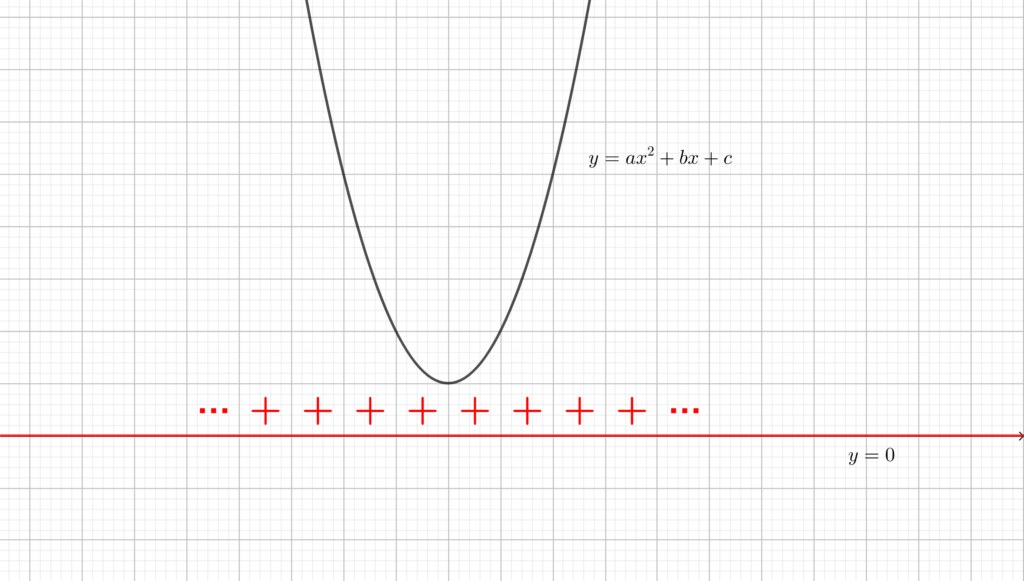
Caso (c) Non essendoci soluzioni dell’equazione di secondo grado associata, la parabola che rappresenta il polinomio non interseca mai la retta $y=0$, e la concavità è verso l’alto (in quanto $a>0$. Il grafico sarà dunque di questo tipo.

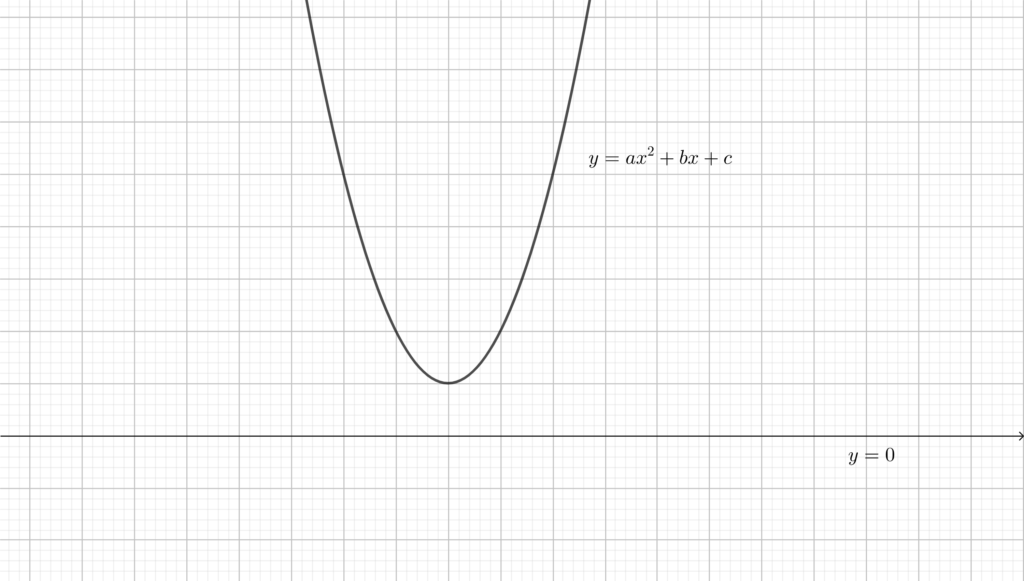
TERZO STEP: LO STUDIO DEI SEGNI DEL POLINOMIO. Quello che dobbiamo fare ora è stabilire per quali $x$ il polinomio sia positivo, per quali negativo e per quali nullo (questa ultima cosa la sappiamo già, avendo determinato le soluzioni dell’equazione di secondo grado). In questo modo saremo pronti per scrivere le soluzioni della disequazione, qualsiasi essa sia. Stabilire il segno, avendo disegnato la parabola, è molto semplice: nelle $x$ tali per cui la parabola è sopra l’asse orizzontale, il polinomio è positivo, nelle $x$ in corrispondenza delle quali la parabola è sotto l’asse orizzontale il polinomio è negativo, mentre nelle $x$ in cui c’è intersezione il polinomio è nullo. Analizziamo separatamente i tre casi.

Caso (a) Analizzando il disegno della parabola e sfruttando l’osservazione precedente, concludiamo che:

Per $x<x_1 v x>x_2$ allora $ax^2+bx+c>0$;
Per $x=x_1 v x=x_2$ allora $ax^2+bx+c=0$;
Per $x_1<x<x_2$ allora $ax^2+bx+c<0$.

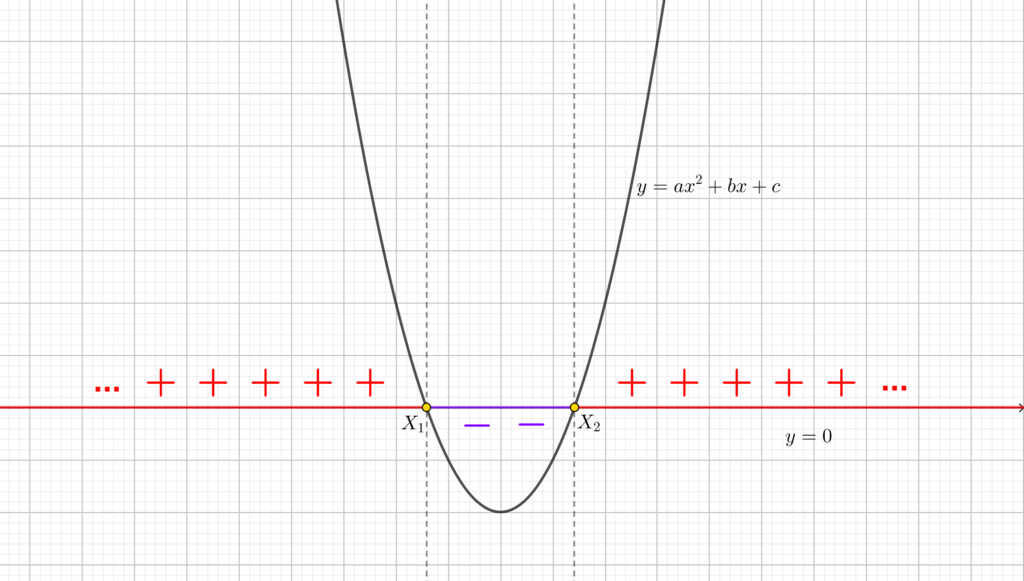
In rosso le $x$ che rendono positivo $ax_2+bx+c$ (se $a>0$), in giallo quelle che lo annullano e in blu quelle che lo rendono positivo, nel caso in cui $\Delta>0$.

Caso (b) In questo caso:

$\forall x\in \mathbb{R}\setminus\{\bar{x}\}$ $ax_2+bx+c>0$;
Se $x=\bar{x}$ allora $ax_2+bx+c=0$;
Per nessuna $x\in\mathbb{R}$ $ax^2+bx+c<0$ (si scrive anche che il sottoinsieme di $\mathbb{R}$ per cui il polinomio è negativo è $\emptyset$).

In rosso le $x$ che rendono positivo $ax_2+bx+c$ (se $a>0), in giallo quelle che lo annullano e in blu quelle che lo rendono positivo, nel caso in cui $latex \Delta=0$.

Caso (c) Chiaramente dal grafico si nota che la parabola è sempre sopra all’asse orizzontale, dunque:

$\forall x\in\mathbb{R}$ accade che $ax^2+bx+c>0$;
Il sottoinsieme dei numeri reali per cui $ax^2+bx+c\le 0$ è $\emptyset$.

Nel caso in cui $a>0$ e $\Delta<0$ la parabola è sempre sopra all’asse orizzontale, dunque il polinomio è sempre positivo.

QUARTO STEP: LA SCRITTURA DELLA SOLUZIONE. Fino ad ora abbiamo agito indipendentemente dal verso della disuguaglianza che compariva nel nostro problema: tuttavia a questo punto dobbiamo prenderla in considerazione, per scrivere la soluzione della nostra disequazione. Avendo davanti il grafico, il trucco è molto semplice: se la disequazione presenta un $\ge$, prenderemo le $x$ rosse e gialle in figura, se presenta un $\le$ quelle blu e gialle , se c’è un $>$ solo le rosse e così via, in modo tale da prendere le $x$ che realizzano il segno del polinomio a noi richiesto dalla disuguaglianza.

Ad esempio, supponiamo la disequazione sia $ax^2+bx+c\ge0$, con $a>0$. Allora:

Se $\Delta>0$ la soluzione è $x\le x_1 \vee x\ge x_2$, e si dice per valori esterni ($S=(-\infty,x_1]\cup[x_2,+\infty)$)
Se $\Delta=0$ la soluzione è $\forall x\in\mathbb{R}$ e la disequazione è sempre verificata ($S=\mathbb{R}$)
Se $\Delta<0$ la soluzione è $\forall x\in\mathbb{R}$ e la disequazione è sempre verificata ($S=\mathbb{R}$) ; dunque accade la stessa cosa.

Facciamo un altro esempio e supponiamo la disequazione sia $ax^2+bx+c\le 0$, con $a>0$ (dovremo prendere in questo caso le $x$ colorate di giallo e blu). Allora:

Se $\Delta >0$ allora la soluzione è $x_1\le x\le x_2$ e si dice per valori interni ($S=[x_1,x_2]$).
Se $\Delta=0$ allora la soluzione è $x=\bar{x}$ e si parla di soluzione isolata ($S=\{\bar{x}\}$).
Se $\Delta<0$ allora la soluzione è $S=\emptyset$ e la disequazione si dice impossibile.

Analogamente si trattano i casi in cui compare $>$ o $<$.

E quando $a<0$?

Fino adesso abbiamo trattato disequazioni del tipo $ax^2+bx+c\ge 0$ (o $ax^2+bx+c\le 0$ o analogamente con $<,>$), supponendo $a>0$. Nel caso in cui $a<0$ si può procedere moltiplicando per $-1$ a sinistra e a destra della disequazione, ricordandosi di cambiare il verso della disequazione, ottenendo:

$ax^2+bx+c\ge 0 \longrightarrow -ax^2-bx-c\le0$.

A questo punto il coefficiente davanti a $x^2$ è diventato positivo e ci troviamo nella casistica precedente.

Se invece uno volesse ragionare direttamente, senza operare questo cambio di segno, i ragionamenti sarebbero gli stessi di prima, però le parabole sarebbero tutte con la concavità (la “pancia”) verso il basso.

Ora facciamo un esempio numerico.

Esercizio.
Risolvere la disequazione $-x^2+x+1< 0$.

Come osservato in precedenza, per tornare al caso in cui il coefficiente davanti a $x^2$ sia positivo, moltiplichiamo per $-1$ a sinistra e a destra della disuguaglianza, cambiandone anche il verso, ottenendo:

$x^2-x-1> 0$.

Questa è la disequazione da risolvere.

PRIMO STEP. Risolviamo l’equazione associata $x^2-x-1=0$. Calcoliamo il $\Delta$:

$\Delta=b^2-4ac=(-1)^2-4\cdot 1 \cdot (-1)=1+4=5$.

Dunque $\Delta=5>0$: ci troviamo nel caso (a), in cui abbiamo due soluzioni distinte, cioè

$x_1=\frac{1-\sqrt{5}}{2}$, $x_2=\frac{1+\sqrt{5}}{2}$.

SECONDO STEP. Essendo nel caso (a), la parabola sarà di questo tipo:

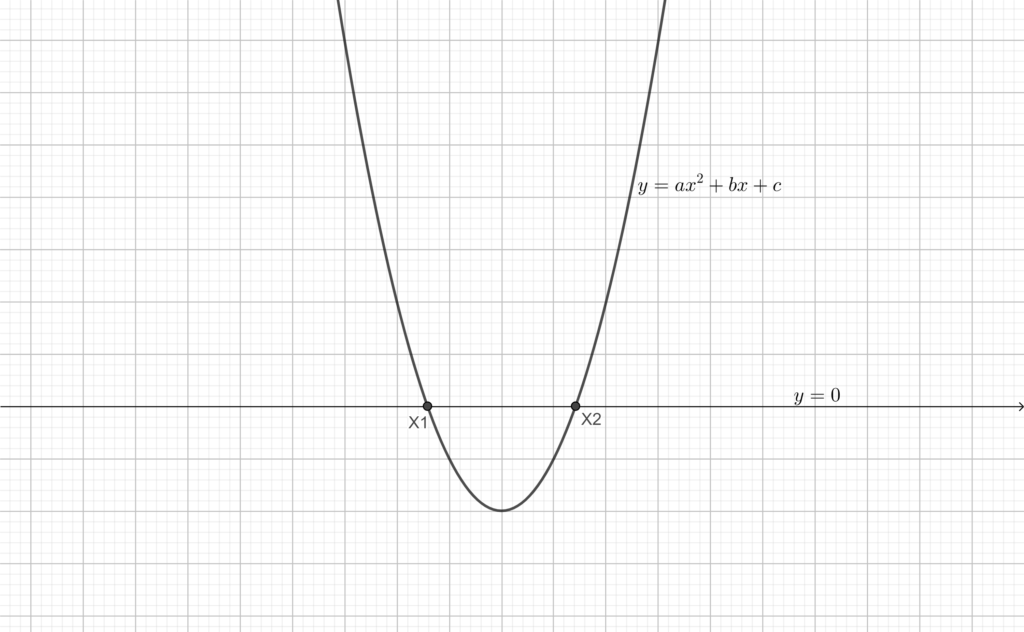
Ecco la parabola, con $x_1=\frac{1-\sqrt{5}}{2}$ e $x_2=\frac{1+\sqrt{5}}{2}$.

TERZO STEP. Analizziamo i segni: guardando il grafico scopriamo che

$x^2-x-1>0$ per $x<\frac{1-\sqrt{5}}{2} \vee x>\frac{1+\sqrt{5}}{2}$
$x^2-x-1=0$ per $x=\frac{1\pm\sqrt{5}}{2}$
$x^2-x-1<0$ per $\frac{1-\sqrt{5}}{2}<x<\frac{1+\sqrt{5}}{2}$.

QUARTO STEP: LA SOLUZIONE. La disequazione da risolvere è $x^2-x-1> 0$, dunque dobbiamo considerare solo i punti rossi, arrivando alla soluzione:

$x< \frac{1-\sqrt{5}}{2} \vee x>\frac{1+\sqrt{5}}{2}$. La disequazione ha soluzione per valori strettamente esterni a $x_1$ e $x_2$.

Prova tu!

Chiaramente abbiamo esaurito tutta la casistica possibile grazie al metodo delle parabole, ma in alcuni casi ci sono metodi più veloci per giungere alla soluzione, perchè basta ricordarsi il comporamento dei polinomi di secondo grado! Ad esempio, se il coefficiente della $x^2$ e la disuguaglianza sono concordi (e $\Delta >0$) la soluzione si ha per valori esterni, se discordi (e $\Delta >0$) per valori interni (prova a controllare che è vero con il metodo delle parabole!) e metodi analoghi si possono usare nelle altre due casistiche: prova a trovarli!

Queste erano le disequazioni di secondo grado!

Speriamo che tu possa aver trovato utile questo nostro articolo. Se hai domande o commenti non esitare a scrivere qui sotto 😉

Clicca qui per condividere!

DISEQUAZIONI DI SECONDO GRADO