Punti di discontinuità

Sapete come determinare e classificare i punti di discontinuità di una funzione?

Per parlare di punti di non continuità, ricordiamo dapprima la definizione di continuità in un punto di una funzione. Consideriamo una funzione \(f \colon (a,b) \to \mathbb{R}\) e sia \(x_0\) un punto appartenente all’intervallo \((a,b)\).

Definizione:
Diciamo che \(f\) è continua nel punto \(x_0\) se esiste \(\lim_{x\to x_0} f(x)\) e vale \(\lim_{x\to x_0} f(x) = f(x_0)\).

Facciamo subito qualche osservazione sulla definizione appena considerata. Chiedere che tale limite esista significa richiedere due cose:

• Che esistano i limiti sinistro e destro, e che questi coincidano;
• Che tale limite sia finito.

Inoltre, chiedere che valga l’uguaglianza \(\lim_{x\to x_0} f(x) = f(x_0)\) significa pretendere che tale limite coincida con il valore assunto dalla funzione nel punto \(x_0\).

Forti di queste considerazioni, possiamo ora classificare i punti di discontinuità di una funzione. Ci sono vari motivi per cui può cadere la proprietà di continuità di \(f\) in un punto:

• Punto di discontinuità di prima specie, o “a salto”: i limiti sinistro e destro esistono, sono entrambi finiti, ma non coincidono;
• Punto di discontinuità di seconda specie: almeno uno tra limite sinistro e destro non esiste oppure è infinito;
• Punto di discontinuità di terza specie, o “eliminabile”: i limiti sinistro e destro esistono, sono finiti, coincidono, ma non coincidono con il valore \(f(x_0)\).

Si noti come questa classificazione sia buona in quanto esaurisce tutti i possibili casi che si possono presentare.

Facciamo subito qualche esempio per capire di cosa stiamo parlando.

Esempio:
Consideriamo la funzione \(f \colon \mathbb{R} \to \mathbb{R}\) definita da

\(f(x)=
\begin{cases}
1 & \text{se} \ x>0,\\
0 & \text{se} \ x=0,\\
-1 & \text{se} \ x<0.
\end{cases}\)

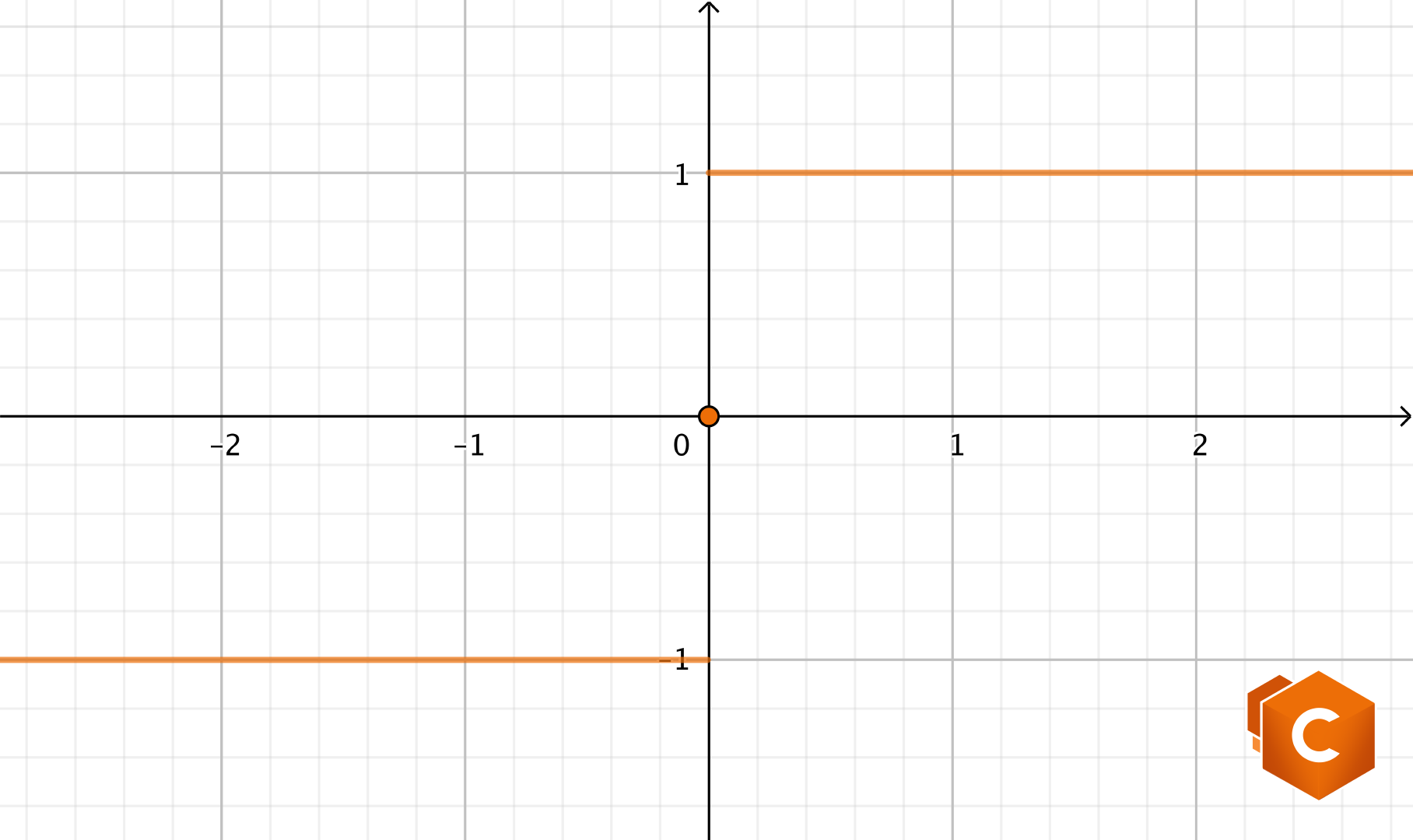
Consideriamo il punto \(x_0=0\); abbiamo che

\(\lim_{x\to 0^-} f(x) = \lim_{x\to 0^-} -1 = -1,\)
\(\lim_{x\to 0^+} f(x) = \lim_{x\to 0^+} 1 = 1.\)

Quindi in questo caso limiti sinistro e destro esistono, sono finiti ma non coincidono! Quindi la funzione ha un punto di discontinuità di prima specie o “a salto”. Solitamente si definisce salto il modulo della differenza tra limite sinistro e destro. In questo caso, dunque, il salto vale \(|1-(-1)|=|1+1|=2.\) Uno sguardo al grafico di questa funzione renderà evidente il significato geometrico del concetto di salto.

Esempio:
Questa volta, consideriamo la funzione \(f \colon \mathbb{R} \to \mathbb{R}\) definita come segue

\(f(x)=
\begin{cases}
e^{\frac{1}{x}} & \text{se} \ x\neq 0,\\
0 & \text{se} \ x=0.
\end{cases}\)

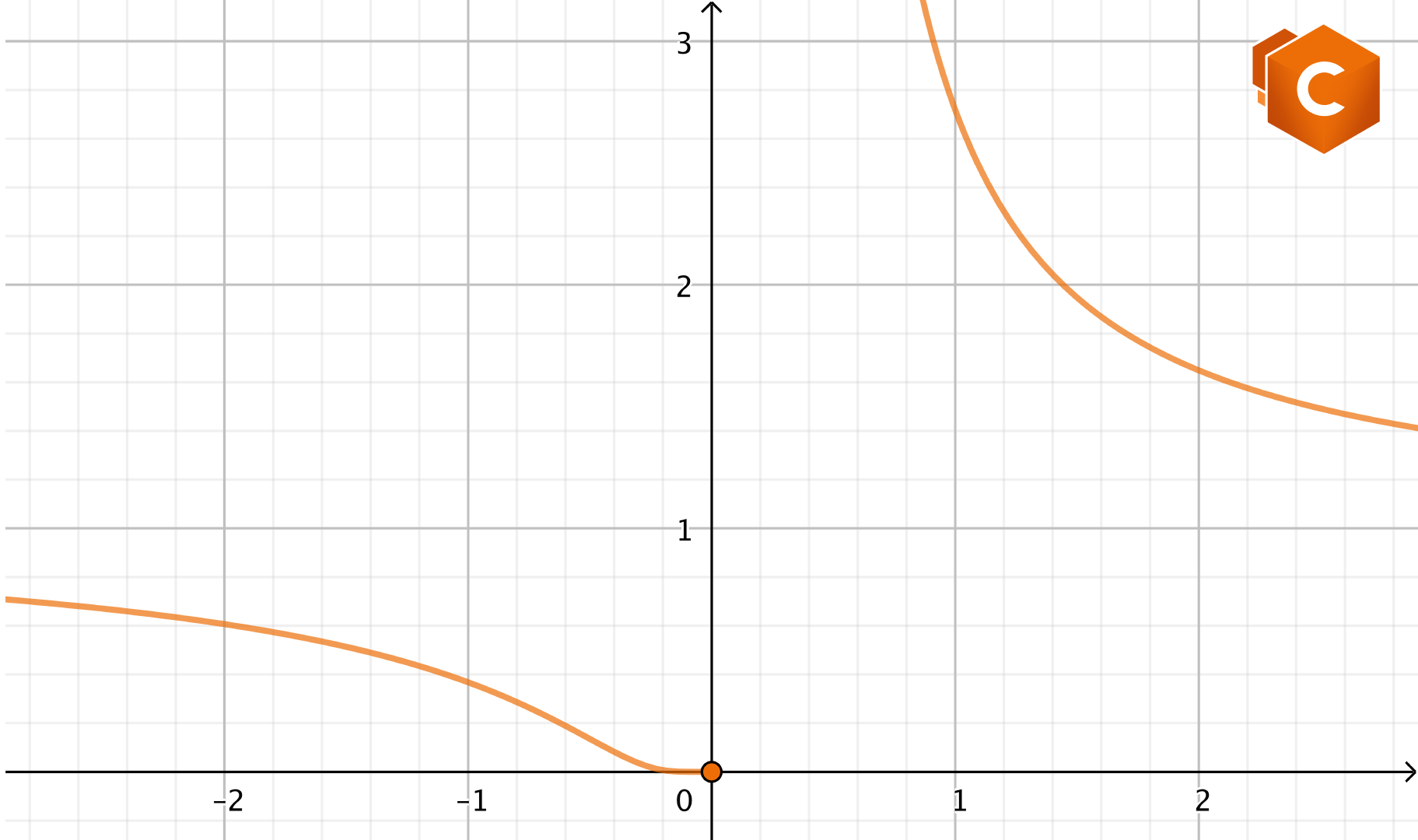
La funzione \(1/x\) tende a infinito per \(x\to 0\). Tuttavia, in base al segno di \(x\), \(1/x\) tende a infinito in modo discorde. Più precisamente:

\(\lim_{x\to 0^{\pm}} \frac{1}{x} = \pm \infty.\)

Sapendo che l’esponenziale ha comportamenti completamente diversi ai “due diversi infiniti”, quanto appena osservato ci suggerisce di calcolare a parte limiti sinistro e destro di \(f(x)\):

\(\lim_{x \to 0^-} f(x) = e^{-\infty}=0,\)
\(\lim_{x \to 0^+} f(x) = e^{+\infty}=+\infty.\)

In questo caso, notiamo che almeno uno (in particolare quello destro) tra limite sinistro e destro non è finito; \(x_0=0\) è dunque un punto di discontinuità di seconda specie.

Esempio:
Un terzo esempio; sia \(f \colon \mathbb{R} \to \mathbb{R}\) definita così:

\(f(x)=
\begin{cases}
x+2 & x>0,\\
1 & x=0,\\
2e^x & x>0.
\end{cases}\)

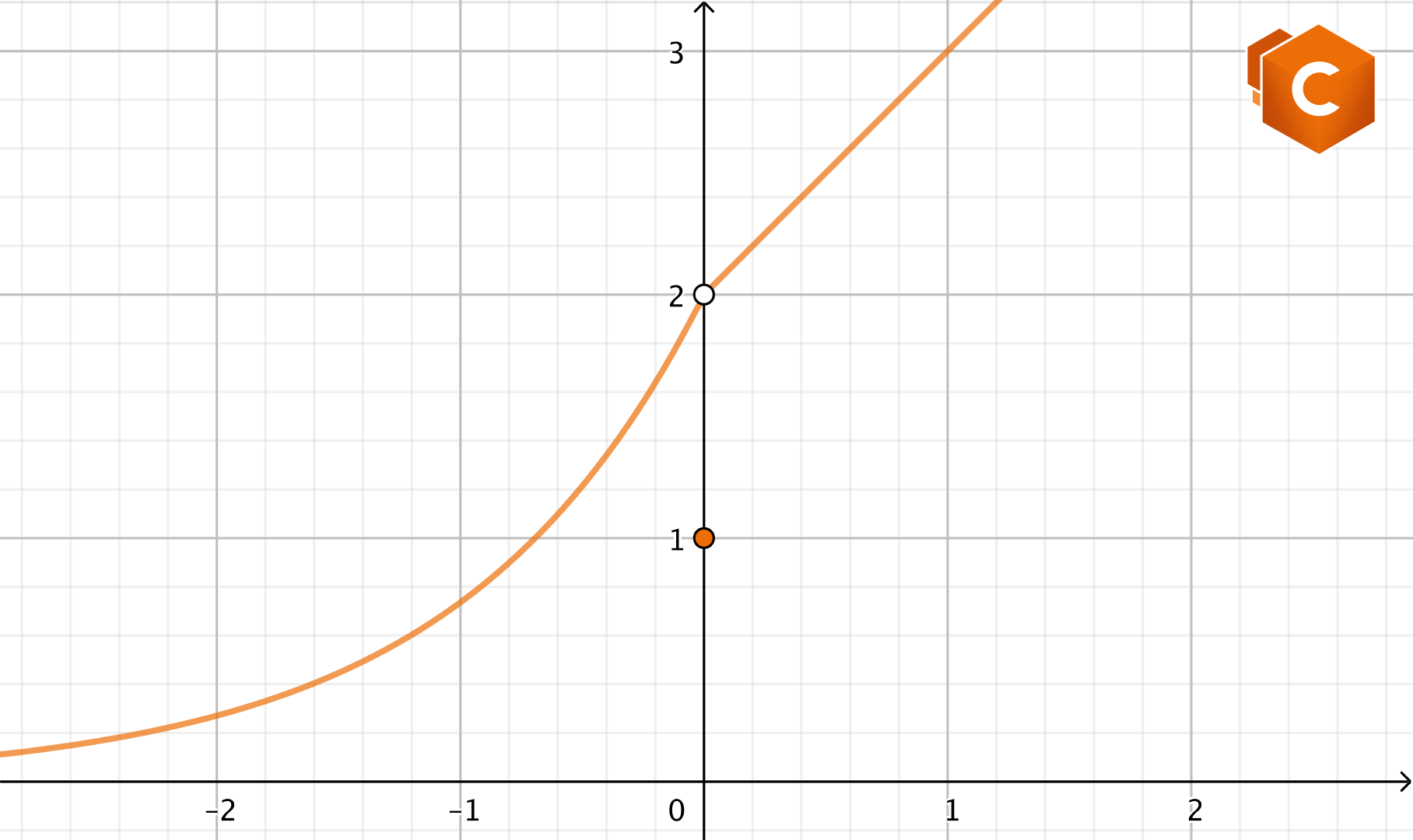
Controlliamo ancora una volta limiti sinistro e destro:

\(\lim_{x\to 0^-} f(x) = \lim_{x\to 0^-} 2e^x= 2,\)
\(\lim_{x\to 0^+} f(x) = \lim_{x\to 0^+} x+2=2.\)

In questo caso limiti sinistro e destro esistono finiti e coincidono! Quindi esiste \(\lim_{x\to 0} f(x)\) e vale 2. Tuttavia \(f(0)=1\) e dunque \(\lim_{x\to 0} f(x) \neq f(0)\), quindi \(f(x)\) ha in \(x_0=0\) una discontinuità di terza specie, o “eliminabile”. Perché si chiama eliminabile? Per il semplice fatto che, in questo caso, è sufficiente modificare il valore della funzione nel punto \(x_0=0\) per rendere la funzione continua! Possiamo rendere esplicita tale modifica:

\(\tilde{f}(x)=
\begin{cases}
f(x) & \text{se} \ x\neq 0,\\
2 & \text{se} \ x=0
\end{cases}
=\)

\(= \begin{cases}
x+2 & x>0,\\
2 & x=0,\\
2e^x & x>0.
\end{cases}\)

Abbiamo ottenuto una nuova funzione \(\tilde{f}(x)\), che differisce da \(f(x)\) solo in un punto, ma che stavolta è continua!

Nota bene!
A volte si parla di punto di discontinuità di una funzione anche se la funzione stessa non è definita nel punto \(x_0\), ma è definita in un suo intorno eccetto solo il punto \(x_0\). Facciamo di nuovo un paio di esempi per chiarire quanto appena detto.

Esempio:
Consideriamo la funzione

\(f(x)=\sin (\frac{1}{x}).\)

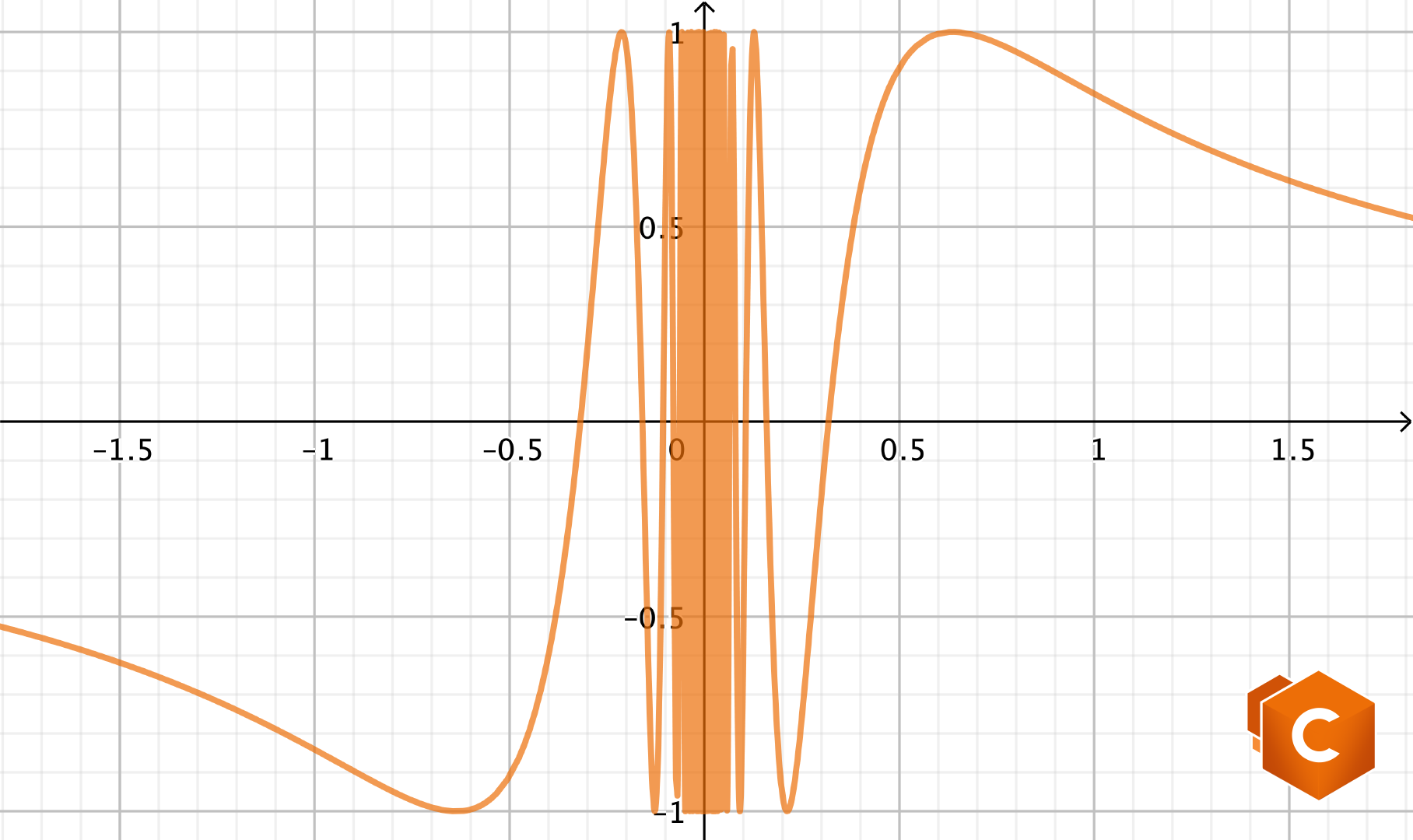
Notiamo subito che la funzione non è definita nel punto \(x_0=0\), ma lo è altrove. Osserviamo inoltre che non esiste \(\lim_{x\to 0} f(x)=\lim_{x\to 0} \sin(\frac{1}{x}).\) Questo perché, per \(x\) che tende a \(0\), \(1/x\) tende ad \(\infty\); tuttavia, \(\sin\) non ammette limite all’infinito (essendo periodica e non costante). Diciamo dunque diciamo che \(x_0=0\) è un punto di discontinuità di seconda specie per \(f(x)\), nel senso che ogni tentativo di prolungamento di \(f(x)\) in \(x_0=0\) genera una funzione che ha effettivamente un punto di discontinuità di seconda specie in \(x_0=0\).

Esempio:
Consideriamo la funzione

\(f(x)= \frac{x^2 – 1}{x-1}.\)

Imponendo la condizione di esistenza sul denominatore, notiamo che \(f(x)\) risulta essere non definita in \(x_0=1\). È però definita altrove, e per \(x\neq 1\) vale

\(f(x)= \frac{(x+1)(x-1)}{x-1}=x+1.\)

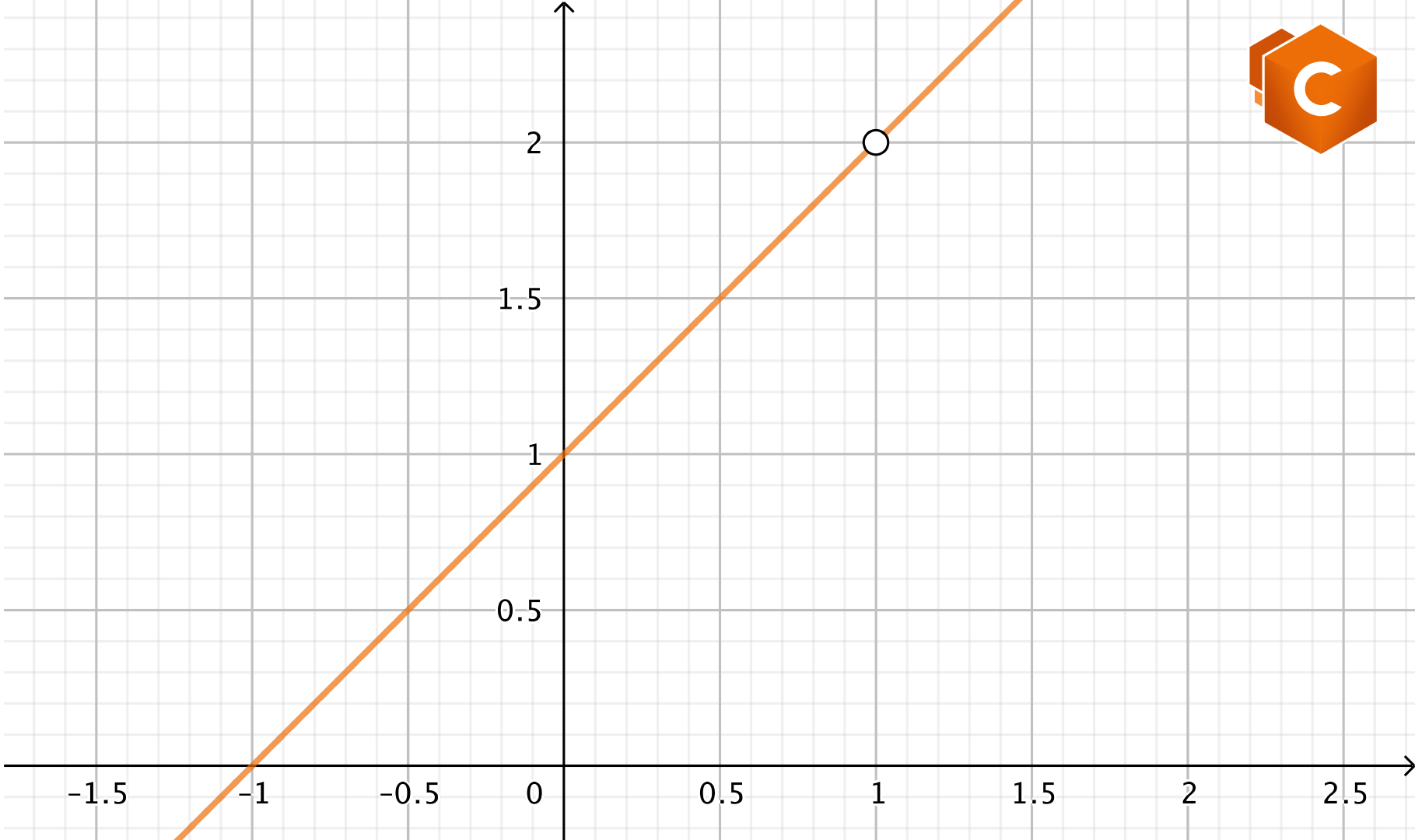
Chiaramente abbiamo \(\lim_{x\to 1} f(x)=\lim_{x\to 1} x+1 =2.\) Dunque diciamo che \(x_0=1\) è un punto di discontinuità di terza specie o “eliminabile”, nel senso che \(f(x)\) non risulta definita in \(x_0=1\), ma esiste un prolungamento di \(f(x)\) in \(x_0=1\) che genera una funzione continua. Tale prolungamento è la funzione \(\tilde{f}(x)\), definita su tutto \(\mathbb{R}\), data da

\(\tilde{f}(x)=
\begin{cases}
f(x) & \text{se} \ x\neq 1,\\
2 & \text{se} \ x=1
\end{cases}
=\)

\(=
\begin{cases}
x+1 & \text{se} \ x\neq 1,\\
2 & \text{se} \ x=1
\end{cases}
=x+1.\)

Questi erano i punti di discontinuità di una funzione 😉
Speriamo tu possa aver trovato utile questo nostro articolo.
Se hai domande o commenti non esitare a scrivere qui sotto!