Retta nel piano cartesiano

Nella lezione di oggi parleremo di uno dei primi argomenti con cui si approccia il piano cartesiano, cioè la retta.

Ricordiamo che il piano cartesiano è costituito da due assi coordinati (\(x\) e \(y\)) con un’origine \(O\). L’obiettivo che abbiamo è quello di studiare una retta all’interno di questo piano, partendo dalla sua equazione analitica (che ne determina tutti i punti), analizzando poi alcune caratteristiche come il coefficiente angolare e il termine noto . Ci soffermeremo, poi, sulle condizioni di parallelismo e perpendicolarità nel piano cartesiano.

Equazione cartesiana implicita della retta

Nel piano cartesiano una retta è individuata da un’equazione di primo grado nelle variabili \(x\) e \(y\), come di seguito:

\(ax+by+c=0\),

dove \(a,b,c\in\mathbb{R}\) e si ha la condizione \((a,b)\neq(0,0)\) perchè altrimenti non comparirebbero nè la \(x\) nè la \(y\) nell’equazione: questa prende il nome di equazione implicita della retta. La relazione tra questa equazione e il grafico della retta è il seguente: dato un punto \(P=(x_P,y_P)\), allora \(P\) è un punto della retta se e solo se le sue coordinate soddisfano l’equazione della retta, cioè \(ax_P+by_P+c=0\). Ad esempio, considerando l’origine \(O=(0,0)\), la retta passa per \(O\) se e solo se \(a\cdot 0+b\cdot 0 +c=0\), cioè \(c=0\): abbiamo scoperto che tutte è sole le rette che passano per l’origine sono quelle con \(c=0\).

Rette orizzontali e rette verticali

Osserviamo, poi, che l’equazione della retta potrebbe dipendere solo da una delle due variabili \(x\) e \(y\), se una tra \(a\) e \(b\) è nulla nell’equazione implicita. Cosa significa ciò?

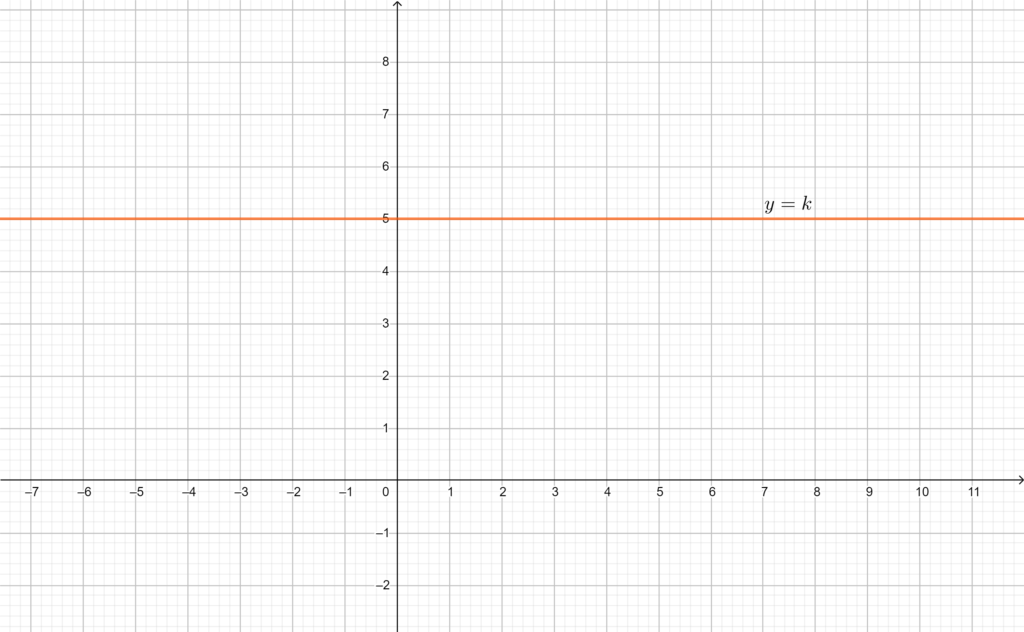
Se \(a=0\) (e di conseguenza \(b\neq 0\)) l’equazione dipende solo da \(y\): infatti ci troviamo di fronte a una retta di equazione implicita \(by+c=0\), dunque \(y=-\frac{c}{b}\). Questo significa che tutti i punti del tipo \(P=(x,-\frac{c}{b})\) soddisfano l’equazione della retta, qualunque sia il valore di \(x\)! Dunque la retta è orizzontale, di ordinata \(-\frac{c}{b}\).

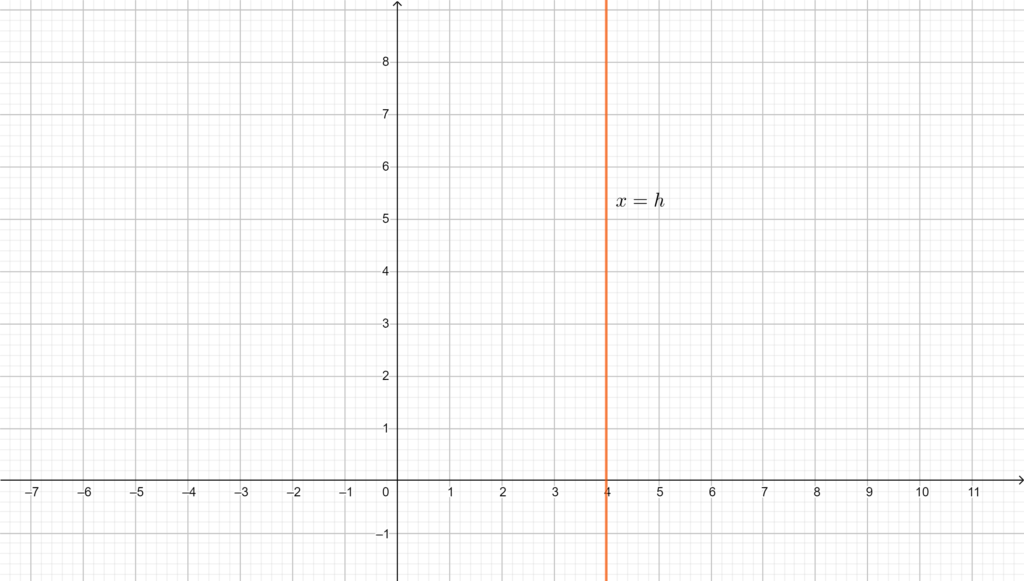
Analogamente, se \(b=0\) (e di conseguenza \(a\neq 0\)) l’equazione dipende solo da \(x\) ed è del tipo \(ax+c=0\), o analogamente \(x=-\frac{c}{a}\). Tutti e soli i punti della retta sono quelli del tipo \(P=(-\frac{c}{a},y)\), qualunque sia il valore di \(y\). La retta è dunque verticale, di ascissa \(-\frac{c}{a}\).

Equazione cartesiana in forma esplicita della retta

Per comprendere un po’ le relazioni tra l’equazione della retta e la geometria è utile scrivere l’equazione stessa in un modo diverso, giungendo alla forma esplicita. Supponiamo che \(b\neq 0\): allora è possibile dividere per \(b\) e isolare la \(y\) giungendo alla scrittura

\(y=-\frac{a}{b}x-\frac{c}{b}\)

Denominando \(m:= -\frac{a}{b}\) e \(q:=-\frac{c}{b}\) giungiamo all’equazione cartesiana in forma esplicita della retta, che è

\(y=mx+q\)

con \(m,q\in\mathbb{R}\). \(m\) prende il nome di coefficiente angolare, mentre \(q\) viene chiamato termine noto.

Geometricamente cosa significa il termine noto?

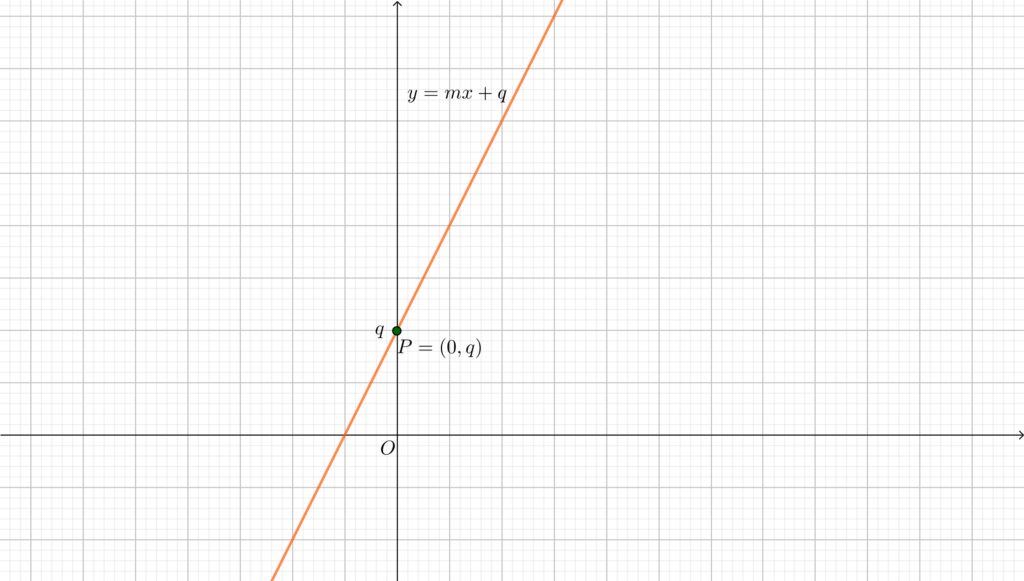
Il termine noto è l’ordinata all’origine, cioè il valore della \(y\) del punto di intersezione tra la retta e l’asse delle \(y\) (di equazione \(y=0\)): infatti è chiaro che, se \(y=mx+q\), allora il punto \(P_0=(0,q)\) soddisfa l’equazione della retta.

In particolare, nel caso in cui l’ordinata all’origine sia \(0\), l’origine \(O=(0,0)\) soddisfa l’equazione della retta. Viceversa, se \(O\) soddisfa l’equazione della retta, deve essere \(q=0\).

Geometricamente cosa significa il coefficiente angolare?

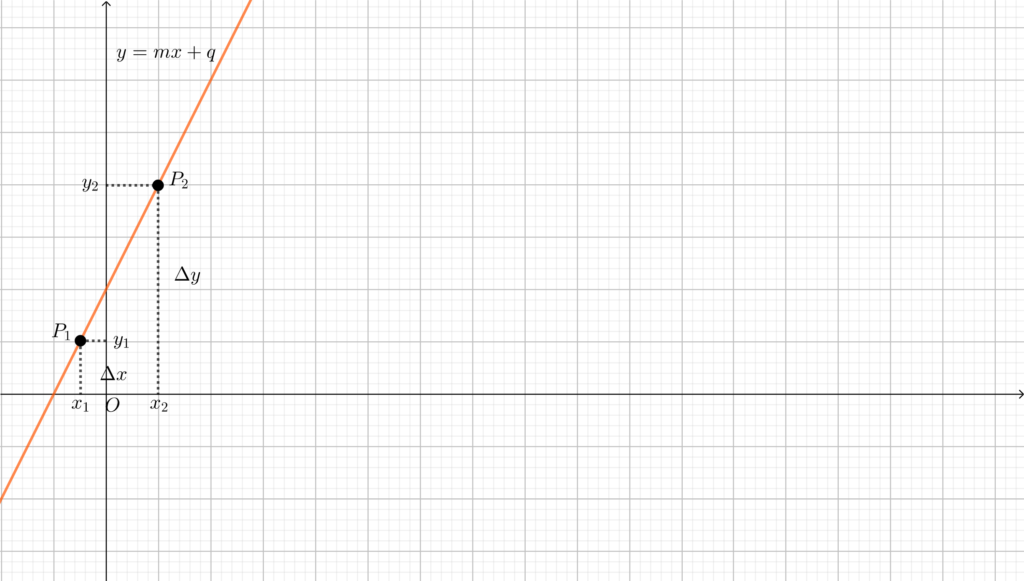
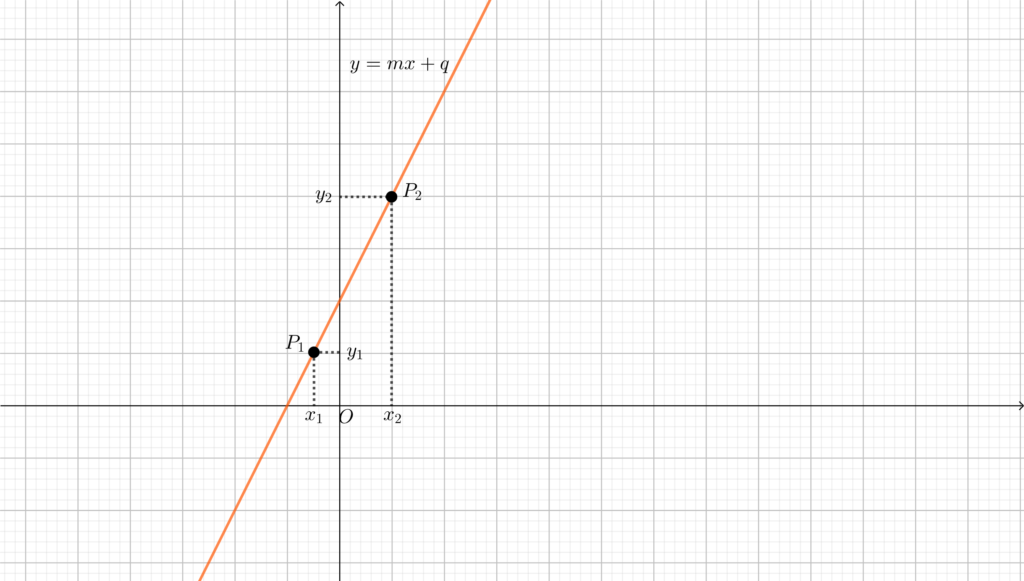
Prendiamo due punti \(P_1=(x_1,y_1)\) e \(P_2=(x_2,y_2)\) appartenenti alla retta di equazione \(y=mx+q\). Questo significa, in particolare, che \(y_1=mx_1+q\) e \(y_2=mx_2+q\). Calcoliamo allora la quantità

\(\frac{\Delta y}{\Delta x}=\frac{y_2-y_1}{x_2-x_1}=\frac{mx_2+q-mx_1-q}{x_2-x_1}=\frac{m(x_2-x_1)}{x_2-x_1}=m\)

Dunque per ogni coppia di punti della retta il rapporto tra la variazione di ordinate e la variazione di ascisse è costante e vale \(m\), il coefficiente angolare: in questo senso il coefficiente angolare descrive l’inclinazione della retta! Maggiore è \(m\) (in valore assoluto), maggiore è l’inclinazione della retta. Inoltre, è anche possibile capire cosa significhino la positività e la negatività di \(m\).

Se \(m>0\) allora per ogni coppia di punti \(\frac{y_2-y_1}{x_2-x_1}>0\), cioè se \(x_2>x_1\) allora anche \(y_2>y_1\): perciò la retta è crescente nelle \(x\) (in parole povere il grafico comincia dalla parte in basso a sinistra del piano cartesiano e poi cresce, toccando sia il terzo che il primo quadrante).

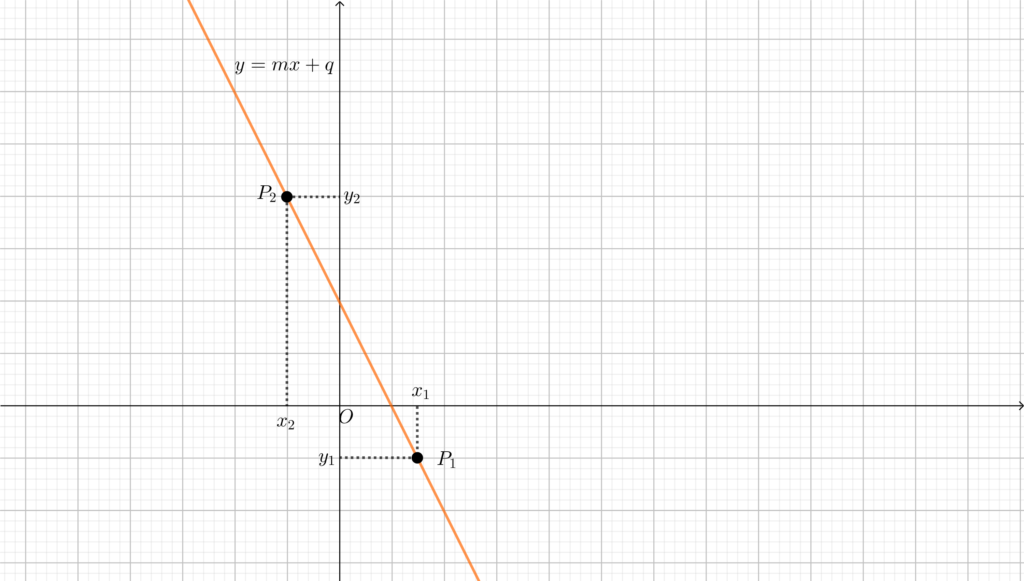
Viceversa se \(m<0\) allora per ogni coppia di punti \(\frac{y_2-y_1}{x_2-x_1}<0\), cioè se \(x_2<x_1\) allora \(y_2>y_1\): perciò la retta è decrescente nelle \(x\) (qui il grafico comincia dalla parte in alto a sinistra del piano cartesiano e poi decresce, toccando sia il secondo che il quarto quadrante).

Se invece \(m=0\), allora l’equazione è del tipo \(y=q\), e non dipende dalle \(x\): come già osservato questo implica che la retta è orizzontale.

Effettivamente con la forma esplicita guadagniamo informazioni geometriche sulla retta, perdiamo un po’ di generalità. Infatti ci sono rette che non possono essere portate a questa forma esplicita, trattasi delle rette verticali. Infatti è chiaro che dalla forma \(y=mx+q\) la dipendenza dalla \(y\) è sempre presente e non possiamo sbarazzarcene: pertanto tutte le rette della forma \(x=k\), cioè le rette verticali, vanno studiate a parte: di queste si dice che il coefficiente angolare sia infinito (a causa del fatto che l’inclinazione è maggiore di quella di tutte le altre rette non verticali).

Alcune rette particolari

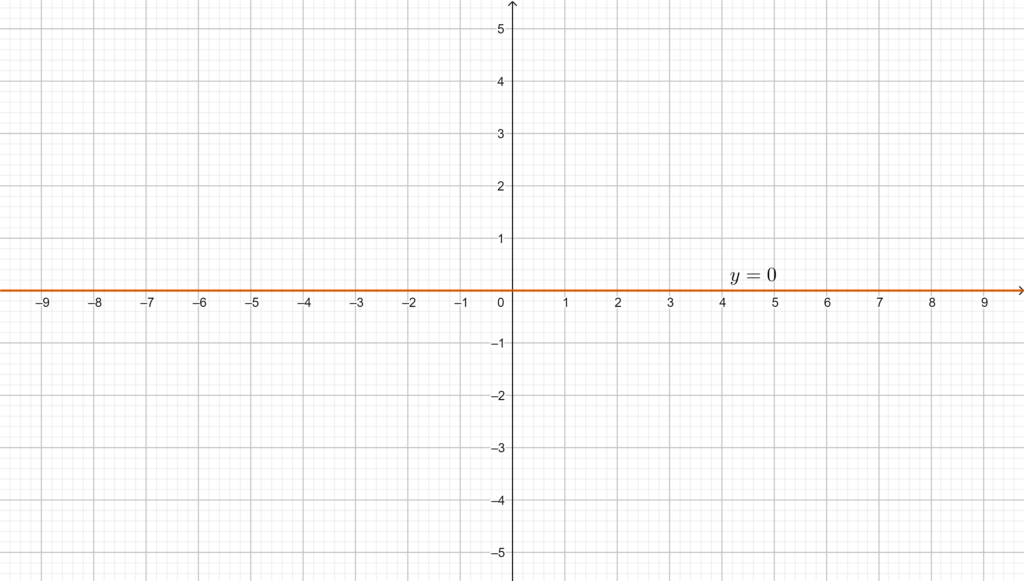
L’asse \(x\), di equazione \(y=0\) (\(m=0\), \(q=0\)).

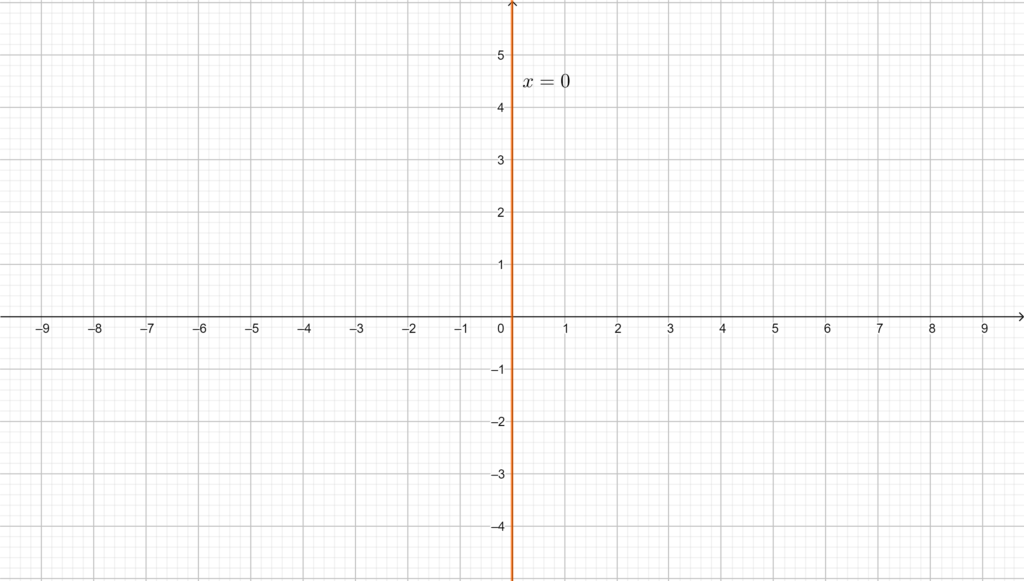
L’asse \(y\), di equazione \(x=0\) (essendo verticale non si esprime in termini di termine noto e coefficiente angolare).

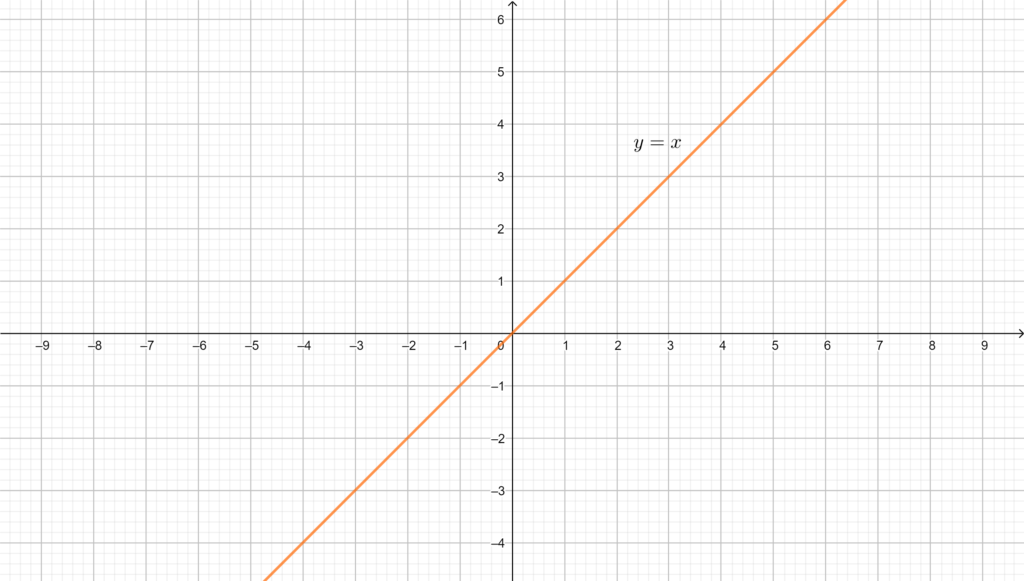
La bisettrice del primo e del terzo quadrante, di equazione \(y=x\) (\(m=1\), \(q=0\)).

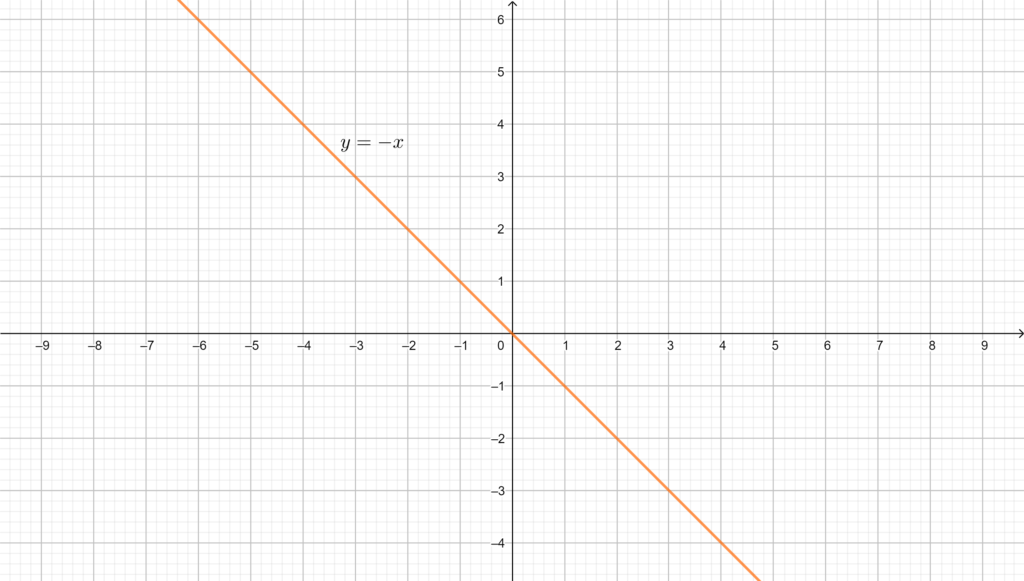
La bisettrice del secondo e del quarto quadrante, di equazione \(y=-x\) (\(m=-1\), \(q=0\)).

Rette parallele e perpendicolari

Come anticipato, è possibile studiare le condizioni di parallelismo e perpendicolarità tra rette utilizzando l’equazione esplicita.

Siano date due rette (non verticali) di equazioni esplicite

\(r_1: y=m_1x+q_1\) e \(r_2: y=m_2x+q_2\).

• Le due rette sono parallele se e solo se hanno la stessa inclinazione, cioè se e solo se hanno lo stesso coefficiente angolare \(m_1=m_2\).
• Le due rette sono perpendicolari se e solo se vale la seguente condizione \(m_1\cdot m_2=-1\), cioè \(m_1=-\frac{1}{m_2}\), uno è l’antireciproco dell’altro.

Uno studio a parte va fatto per le rette verticali \(x=k\), perchè, come già detto, queste non sono scrivibili in forma esplicita: tuttavia questo studio è molto semplice:

• Una retta è parallela a una retta verticale se e solo se è anch’essa verticale, cioè della forma \(x=h\).
• Una retta è perpendicolare a una retta orizzontale se e solo se è orizzontale, cioè della forma \(y=h\).

Queste erano le rette nel piano cartesiano!

Speriamo che tu possa aver trovato utile questo nostro articolo. Se hai domande o commenti non esitare a scrivere qui sotto 😉