Un’altra funzione “sinuosa”

Nell’articolo di oggi cercheremo di risolvere un esercizio relativo a un’altra funzione dall’andamento sinuoso. In particolare risolveremo alcune richieste che richiedono metodi meno “standard” del solito per giungere alla conclusione. Ovviamente si invita il lettore a provare inizialmente a rispondere alle richieste autonomamente, consultando solo successivamente la soluzione qui proposta.

Sia data la funzione \(f(x)=\sin{x} – x\cos{x}\). Dimostrare le seguenti affermazioni:

a) \(f\) è una funzione dispari;

b) Per \(x\in (0,\pi]\) \(f(x)>0\);

c)\(\exists{!} x_0\in(0,2\pi]\) t.c. \(f(x_0)=0\).

Successivamente si tracci il grafico di \(f\) per \(x\in [-5\pi,5\pi]\).

a) Ricordiamo che una funzione \(f(x)\) si dice dispari se \(f(x)=-f(-x)\) \(\forall x\in D\), dove \(D\) è il dominio della funzione. Geometricamente questa condizione equivale alla richiesta che il grafico della funzione è simmetrico rispetto all’origine. Nel nostro caso il dominio della funzione è \(D=\mathbb{R}\), dunque andiamo a verificare la condizione di disparità per un generico \(x\in \mathbb{R}\). Ricordando le proprietà trigonometriche di seno e coseno, valgono \(\sin{-x}=-\sin{x}\) e \(\cos{-x}=\cos{x}\), dunque:

\(f(-x)=\sin{-x} – (-x)\cos{-x}=-\sin{x}-(-x)\cos{x}=-\sin{x}+x\cos{x}=\)

\(=-(\sin{x}-x\cos{x})=-f(x)\).

Abbiamo mostrato che \(f(-x)=-f(x)\), quindi la disparità.

(b) Il metodo “standard” per dimostrare che \(f(x)>0\) quando \(x\in (0,\pi]\) è quello di studiare il segno della funzione, cioè analizzare la disequazione \(\sin{x}-x\cos{x}>0\), tuttavia, il fatto che questa mette insieme una funzione polinomiale come \(x\) con funzioni trigonometriche rende difficile la risoluzione diretta di questa disequazione. Proviamo a ragionare allora in un modo alternativo.

Facilmente si può osservare che \(f(0)=\sin{0}-0\cos{0}=0\): dunque, fatta questa osservazione, se riuscissi a mostrare, ad esempio, che \(f\) cresce \(\forall x\in(0,\pi]\) (o analogamente che decresce) avrei finito! Come è noto in base ai risultati teorici, la monotonia della funzione \(f\) è strettamente collegata al segno della sua derivata, che andiamo a calcolare.

\(f'(x)=\cos{x}-(\cos{x}-x\sin{x})=x\sin{x}\).

Studiamo allora \(f'(x)>0\), cioè \(x\sin{x}>0\). Questa è una disequazione molto più facile da trattare della precedente nell’intervallo \((0,\pi]\). Infatti in questo intervallo \(x\) è sempre positivo, dunque il segno della disequazione dipende solo dal segno di \(\sin{x}\) e la disequazione si trasforma perciò in \(\sin{x}>0\). Come si nota dal grafico della funzione \(\sin{x}\) in figura, è chiaro che in \((0,\pi]\) questa è positiva. Dunque \(f'(x)>0 \forall x\in(0,\pi]\), quindi \(f(x)\) è strettamente crescente in tale intervallo.

In conclusione \(\forall x\in(0,\pi] f(x)>f(0)=0\), come volevasi dimostrare.

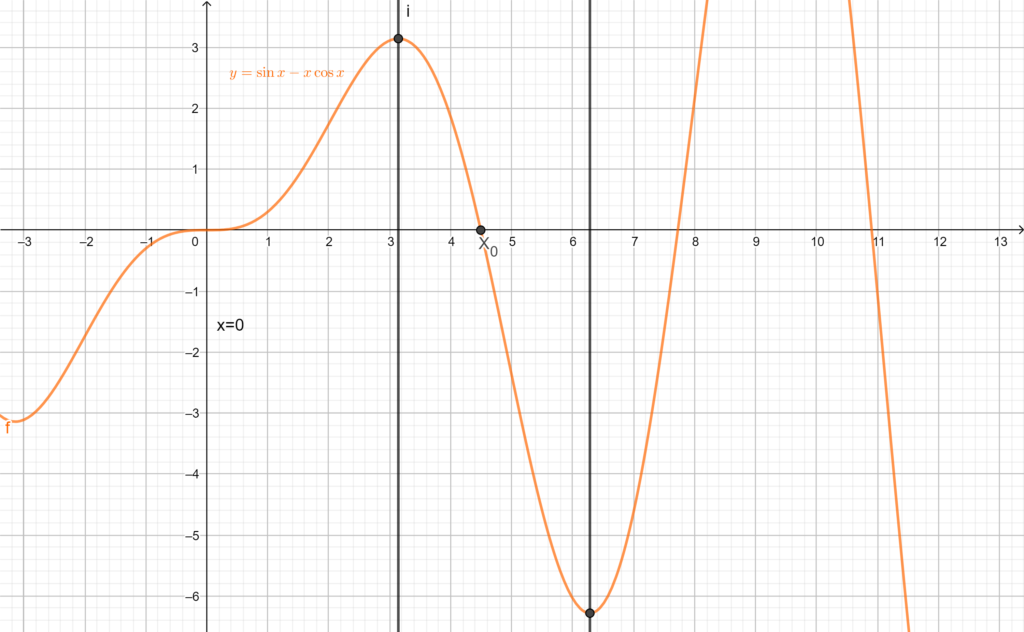
(c) Vogliamo mostrare che esiste un unico \(x_0\in(0,2\pi]\) tale che \(f(x_0)=0\). La prima domanda è la seguente: dove sarà questo zero? Di sicuro non ce ne è alcuno in \((0,\pi]\), dato che abbiamo dimostrato che in quell’intervallo la funzione è strettamente positiva. Dunque dobbiamo dimostrare che ce ne è uno solo tra \(\pi\) e \(2\pi\). La richiesta dunque diventa:

“Dimostra che \(\exists{!} x_0\in[\pi,2\pi]\) tale che \(f(x_0)=0\)”.

Da come è posta la richiesta sembra essere utile il teorema degli zeri. Questo afferma che, data una funzione \(f(x)\) continua su \([a,b]\) tale che \(f(a)f(b)<0\) (equivalentemente \(f(a)\) e \(f(b)\) sono discordi), allora esiste almeno un \(x_0\in(a,b)\) tale che \(f(x_0)=0\). Nel nostro caso l’intervallo è \([\pi,2\pi]\), su cui \(f\) è chiaramente continua. L’unica cosa che ci resta da mostrare è che \(f(\pi)\) e \(f(2\pi)\) sono discordi. Effettivamente \(f(\pi)>0\) (come dimostrato nel punto b) ) e \(f(2\pi)=\sin{2\pi}-2\pi\cos{2\pi}=0-2\pi=-2\pi<0\). Le ipotesi sono verificate, quindi esiste almeno un \(x_0\in[\pi,2\pi]\) che sia uno zero della funzione.

Dobbiamo ora mostrare che questo è unico: per farlo è sufficiente far vedere che la funzione è monotona nell’intervallo \([\pi,2\pi]\): analogamente a quanto fatto nel punto precedente studiamo il segno della derivata \(f'(x)\) in \([\pi,2\pi]\). \(f'(x)=x\sin{x}\). Essendo nell’intervallo considerato \(x>0\), studiamo il segno di \(\sin{x}\), che in \([\pi,2\pi]\) è negativa. Perciò la derivata prima di \(f\) è negativa nel nostro intervallo, dunque la \(f\) è monotona decrescente. Lo zero deve essere unico!

La richiesta successiva è quella di tracciare il grafico della funzione nell’intervallo \([-5\pi,5\pi]\). A tal proposito è utile utilizzare la disparità della funzione \(f\), dimostrata al punto a) per dimezzare il lavoro da fare: infatti è sufficiente tracciare il grafico di \(f\) in \([0,5\pi]\) e poi estenderlo agli \(x\) negativi per simmetria rispetto all’origine. Lavoriamo allora per \(x\in[0,5\pi]\). Analizziamo innanzitutto il segno di \(f'(x)=x\sin{x}\), che, come già osservato, è più facile da studiare rispetto al segno di \(f\). Essendo \(x>0\) in \([0,5\pi]\), il segno di \(f’\) coincide con il segno di \(\sin{x}\). Perciò, come si nota in figura, il segno della derivata (e conseguentemente la monotonia della funzione) è così schematizzato:

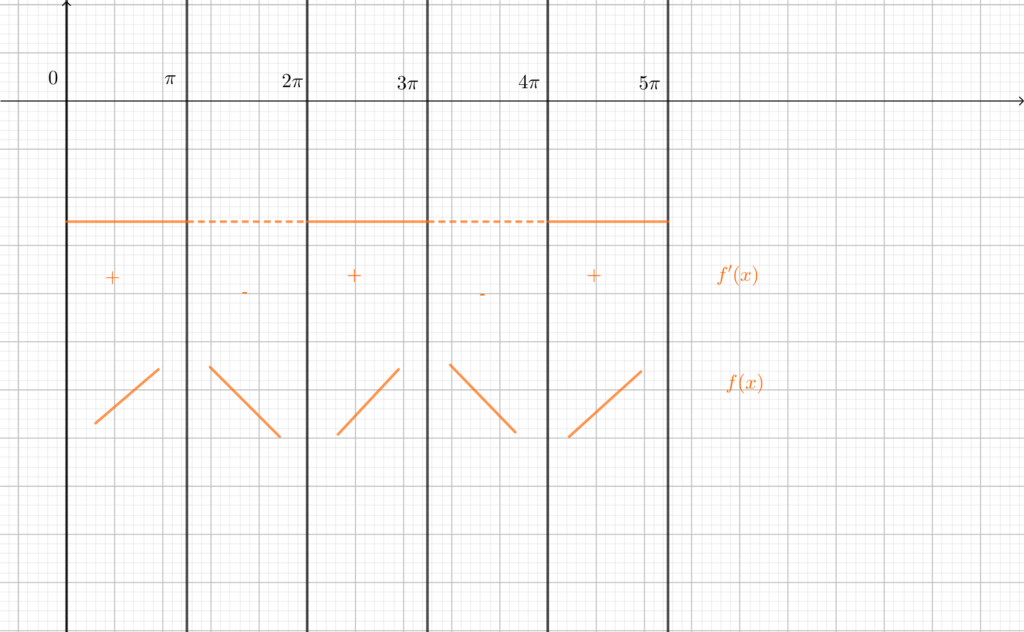
Risulta evidente che i punti del tipo \(x=(2k+1)\pi\) sono punti di massimo relativo, mentre i punti del tipo \(x=2k\pi\) sono punti di minimo relativo. Tra un punto di massimo e un punto di minimo la funzione è monotona, dunque sulla falsariga di quanto abbiamo fatto nel punto c), se riuscissimo a mostrare che due punti stazionari consecutivi hanno immagine di segno opposto, il teorema degli zeri e la monotonia della funzione garantirebbero che esiste un unico zero tra due punti stazionari consecutivi. In effetti

• \(f((2k+1)\pi)=\sin{(2k+1)\pi}-(2k+1)\pi\cos{(2k+1)\pi}=+(2k+1)\pi>0\) (i punti di massimo relativo hanno immagine positiva);
• \(f(2k\pi)=\sin{2k\pi}-2k\pi\cos{2k\pi}=-2k\pi<0\) (i punti di minimo relativo hanno immagine negativa).

Perciò, come già accennato, per ogni intervallo del tipo \([2k\pi,(2k+1)\pi] \exists{!} x_k\in[2k\pi,(2k+1)\pi]\) tale che \(f(x_k)=0\) (analogamente per gli intervalli del tipo \([(2k-1)\pi,2k\pi]\)).

Siamo quindi pronti per tracciare il grafico della funzione in \([0,5\pi]\) e, conseguentemente, in \([-5\pi,5\pi]\).

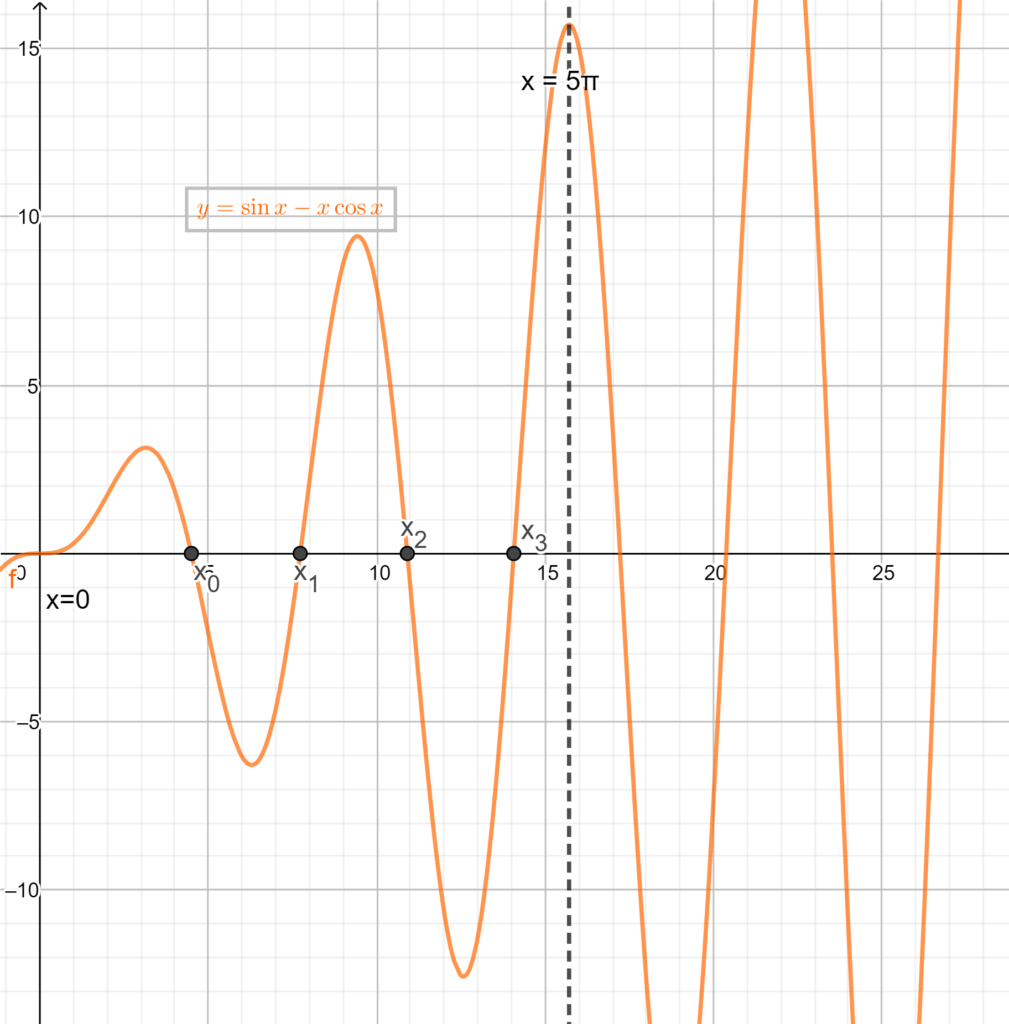
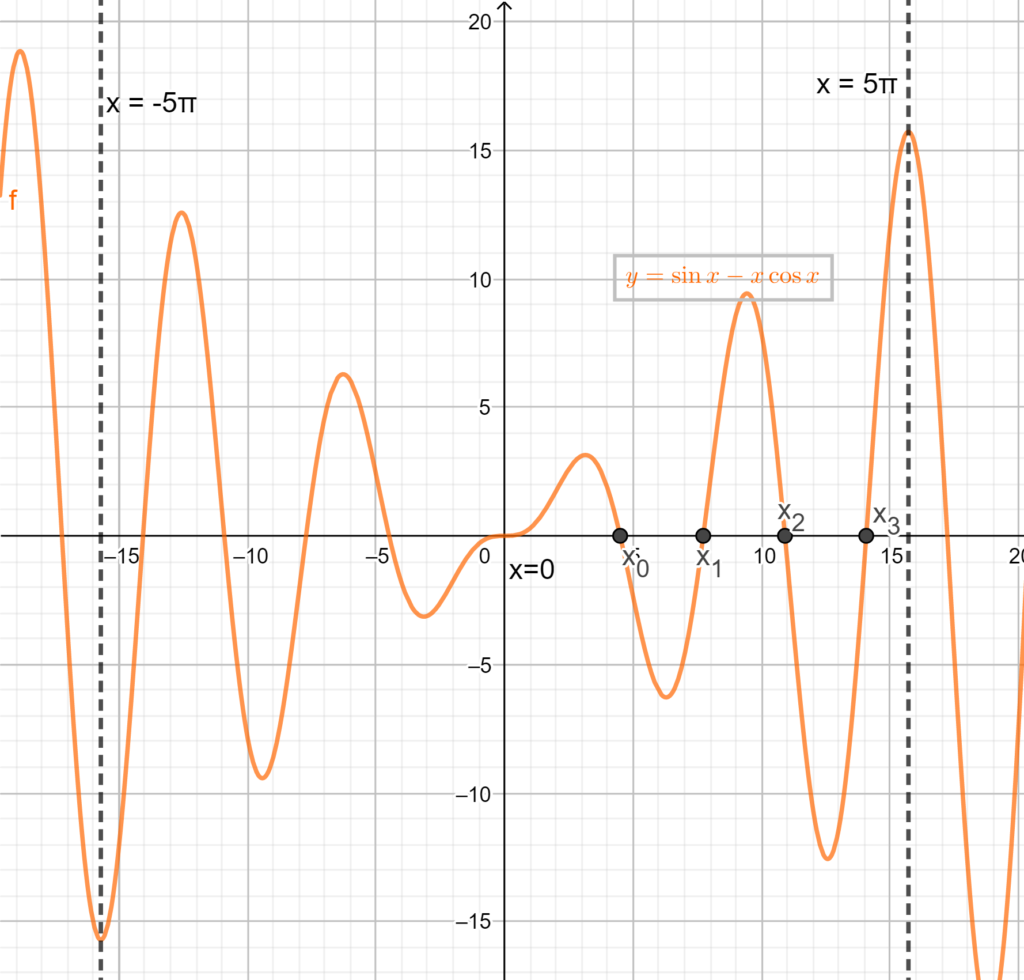
Prima di concludere, lasciamo ai lettori che sono arrivati fino a questo punto un ulteriore esercizio “bonus”, da provare a svolgere da soli.

Dimostrare che i massimi relativi del grafico di \(f^2(x)\) giacciono su una parabola, mentre i suoi minimi relativi su una retta. Si scrivano le equazioni della parabola e della retta.

Questo era un esercizio su una funzione dall’andamento sinuoso  😉
Speriamo tu possa aver trovato utile questo nostro articolo.
Se hai domande o commenti non esitare a scrivere qui sotto! Non esitare a scrivere qualche idea per la soluzione dell’esercizio “bonus”!