Il Teorema di Rolle

Quanta familiarità hai con questo teorema? Secondo te cosa succederebbe se provassimo a togliere alcune delle sue ipotesi?

Sia \(f\) una funzione definita su un intervallo \([a,b]\) a valori reali, tale che \(f\) soddisfi le seguenti ipotesi:

1. \(f(x)\) è continua in ogni punto \(x\in [a,b]\);
2. \(f(x)\) è derivabile in ogni punto \(x\in (a,b)\);
3. f(a)=f(b).

Allora \(\exists x\in (a,b)\) tale che \(f'(x)=0\)

Questo è l’enunciato del teorema di Rolle. Ricordandoci che un punto \(x\) in cui \(f\) è derivabile e la sua derivata prima è nulla si dice punto stazionario, il teorema di Rolle afferma che le condizioni (1)-(2)-(3) sono sufficienti perchè sia presente un punto stazionario per \(f\) in \((a.b)\). Vediamo alcuni esempi di applicazione di questo teorema.

Esempio 1

Sia \(f(x)=\sin{x}\) definita nel suo periodo \([0,2\pi]\). Esiste (almeno) un punto stazionario per \(f\) in \([0,2\pi]\)?

Possiamo procedere in due modi: il primo è quello di calcolare esplicitamente la derivata \(f'(x)\) e verificare che vi siano punti in cui questa si annulla. Il secondo metodo sfrutta il teorema di Rolle: verifichiamo cioè che \(f\) soddisfa le ipotesi (1)-(2)-(3), così che il teorema appena enunciato ci garantisca,senza fare conti, la presenza di un punto stazionario!

(1) \(f\) è continua in \([0,2\pi]\)? Sì, infatti per ogni \(x_0\in [0,2\pi] \lim_{x\to x_0} \sin{x} = \sin{x_0}\).

(2) \(f\) è derivabile in \((0,2\pi)\)? Sì, infatti per ogni \(x_0\in (0,2\pi)\) vale che

\(lim_{h\to 0} \frac{\sin{x_0+h}-\sin{x_0}}{h} = \)

\(=lim_{h\to 0} \frac{\sin{x_0}\cos{h}+\cos{x_0}\sin{h}-sin{x_0}}{h}\)

, usando le formule di addizione. Poi, raccogliendo \(\sin{x_0}\) e ricordando che \(lim_{h\to 0} \frac{\cos{h}-1}{h}=0\), si ottiene

\(lim_{h\to 0} \frac{\sin{x_0+h}-\sin{x_0}}{h}=\cos{x_0}.\)

Dunque il limite esiste finito e \(f\) è derivabile.

(3) \(f(0)=f(2\pi)\)? Chiaramente ciò è vero, in quanto \(\sin{0}=\sin{2\pi}=0\).

Dunque il teorema di Rolle garantisce la presenza di \(x_0\in(0,2\pi)\) tale per cui \(f'(x_0)=0\). Se volessimo capire effettivamente quanto vale \(x_0\) potremmo scegliere uno qualsiasi dei punti in cui la funzione derivata \(f'(x)\) si annulla. Nel nostro caso è chiaro che, poichè \(f(x)=\sin{x}\), allora

\(f'(x)=\cos{x}\), che in \((0,2\pi)\) si annulla in \(x=\frac{\pi}{2}\) e in \(x=\frac{3}{2}\pi\). Dunque possiamo scegliere,ad esempio, \(x_0=\frac{\pi}{2}\) come punto stazionario.

Questo esempio ci mostra infatti come le ipotesi del Teorema di Rolle ci garantiscono l’esistenza di un punto sazionario, non la sua unicità!

Esempio 2

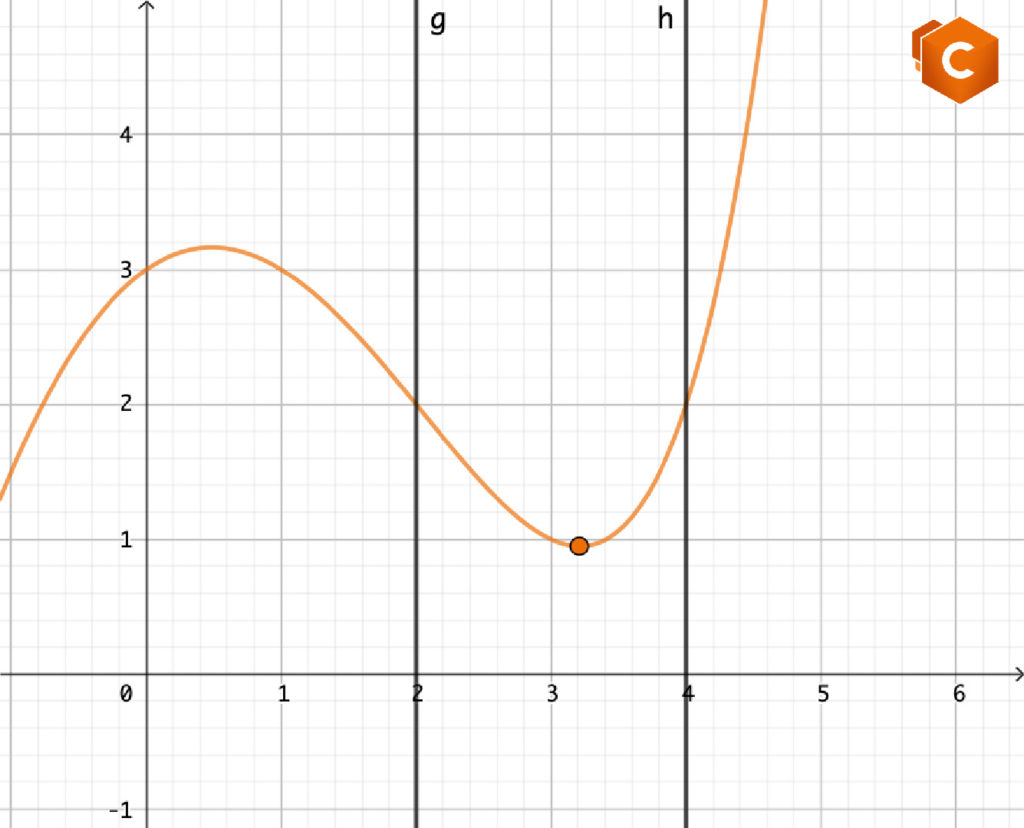
Stabilire se la funzione \(f(x)=2^x-x^2+2\) ammette punti stazionari in \([2,4]\).

Mentre nell’esempio precedente, anche senza utilizzare il teorema di Rolle ce la si poteva cavare, poichè non era difficile calcolare gli zeri di \(f'(x)=\cos{x}\), in questo caso la derivata prima di \(f\) è \(f'(x)=\ln(2)\cdot  2^x-2x\) e il calcolo esplicito dei suoi zeri in \([2,4]\) può dare dei problemi. Affidicamoci allora al teorema di Rolle! 

Le ipotesi (1) e (2) sono verificate, in quanto \(f\) è somma di funzioni continue e derivabili, dunque è continua in \([2,4]\) e derivabile in \((2,4)\).

(3) è verificata. Infatti:

\(f(2)=2^2-2^2+2=2\)

\(f(4)=2^4-4^2+2= 16-16+2=2\).

Perciò il teorema di Rolle garantisce l’esistenza di \(x_0\in(2,4)\) tale che \(f'(x_0)=0\). 

Controesempi

Quello che ci apprestiamo a fare ora è la seguente cosa: toglieremo a una a una le ipotesi (1)-(2)-(3): ci chiediamo allora se valga la tesi, cioè se f ammette un punto stazionario in \([a,b]\).

Controesempio 1

Se \(f\) non soddisfa (1), ma soddisfa (2) e (3) possiamo comunque concludere che \(f\) ammette un punto stazionario in \([a,b]\)?

Assolutamente no! Ad esempio, sia data la funzione definita in \([0,1]\)
\(f(x)=
\begin{cases}
x^3 & \text{se} \ x\in (0,1],\\
1 & \text{se} \ x=0.
\end{cases}\)                        

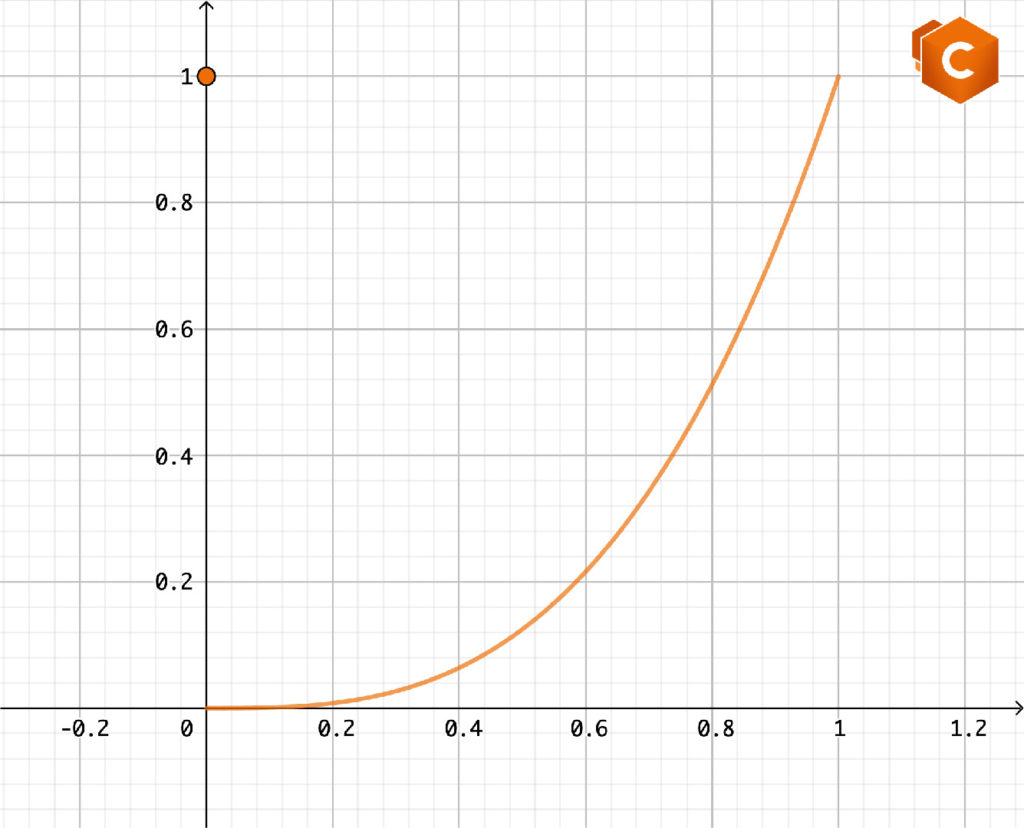
(1) non vale. Infatti \(f\) non è continua in \(x=0\). In effetti \(\lim_{x\to0^+}f(x)=0\), mentre \(f(0)=1\).

(2) vale. Infatti in \((0,1) \ f\) è definita come una cubica, che è derivabile.

(3) vale. Infatti \(f(0)=f(1)=1\).

Tuttavia non sono presenti punti stazionari per \(f\) in \((0,1)\). Infatti in \((0,1)\) la derivata di \(f\) è \(f'(x)=3x^2\), strettamente positiva.

Controesempio 2

Cerchiamo ora di negare la seconda ipotesi, pur mantenendo vere la prima e la terza. Anche in tale circostanza non possiamo, però, garantire la presenza di un puno stazionario.

Ad esempio sia \(f(x)=|x|\), considerata nell’intervallo \([-1,1]\).

Chiaramente (1) vale, poichè la funzione è continua. Inoltre \(f(-1)=|-1|=1=|1|=f(1)\), quindi anche (3) è verificata. Tuttavia (2) non vale in questo caso. Infatti 
\(f'(x)=
\begin{cases}
-1 & \text{se} \ x\in (-1,0),\\
1 & \text{se} \ x\in (0,1).
\end{cases}\).

Dunque risulta evidente che non esiste \(\lim_{x\to0} f'(x)\), in quanto \(-1=\lim_{x\to0^-}f'(x)\neq\lim_{x\to0^+}f'(x)=1\). Quindi \(x=0\) è punto di non derivabilità per \(f\), e \(f\) non è derivabile in \((-1,1)\).

Anche in questo caso non è presente alcun punto stazionario per \(f\), in quanto la derivata di \(f\), laddove esiste, è 
\(f'(x)=
\begin{cases}
-1 & \text{se} \ x\in (-1,0),\\
1 & \text{se} \ x\in (0,1).
\end{cases}\) e non si annulla (non è nemmeno derivabile!).

Controesempio 3

Nel caso in cui valgano (1) e (2) ma non (3) si può dire qualcosa riguardo all’esistenza dei punti stazionari? Anche in questo caso non si può concludere che i punti stazionari esistono, in quanto si possono fornire esempi di funzioni continue, derivabili e iniettive prive di punti stazionari.

Sia ad esempio \(f(x)=x\) per \(x\in[0,1]\). Poichè le funzioni polinomiali sono continue e derivabili (1) e (2) sono verificati. (3) è falsa in quanto \(0=f(0)\neq f(1)=1\). Tuttavia non ci sono punti stazionari, in quanto \(f'(x)=1\) e non si annulla mai in \((0,1)\).

Questi controesempi ci fanno comprendere come ciascuna delle tre ipotesi del teorema di Rolle siano fondamentali. 

Nota bene

I controesempi mostrati potrebbero far sorgere il sospetto che il teorema di Rolle sia una condizione non solo sufficiente, ma anche necessaria, per garantire la presenza di punti stazionari. Questa intuizione risulta però sbagliata, e un semplice esempio mostrerà come il teorema di Rolle sia solo una condizione sufficiente ma non necessaria. Consideriamo la funzione \(f(x)=x^2\) definita sull’intervallo \([-1,2]\). Chiaramente (3) non è verificata in quanto \(f(-1)=1\neq 4=f(2)\), ma \(f'(x)=2x\) si annulla per \(x=0\in (-1,2)\), e dunque \(f\) ha un punto stazionario nell’intervallo considerato, nonostante le ipotesi del teorema di Rolle non siano verificate!

Questi era il Teorema di Rolle 😉
Speriamo tu possa aver trovato utile questo nostro articolo.
Se hai domande o commenti non esitare a scrivere qui sotto!